Derivatives of Exponential and Logarithmic Functions

Section 3.9 Derivatives of Exponential and Logarithmic Functions

Learning Objectives.

Find the derivative of exponential functions.
Find the derivative of logarithmic functions.

So far, we have learned how to differentiate a variety of functions, including trigonometric, inverse, and implicit functions. In this section, we explore derivatives of exponential and logarithmic functions. As we discussed in Exponential and Logarithmic Functions 1.7, exponential functions play an important role in modeling population growth and the decay of radioactive materials. Logarithmic functions can help rescale large quantities and are particularly helpful for rewriting complicated expressions.

Subsection 3.9.1 Derivative of the Exponential Function

Just as when we found the derivatives of other functions, we can find the derivatives of exponential and logarithmic functions using formulas.

We know that $2.7182\lt e\lt 2.7183.$

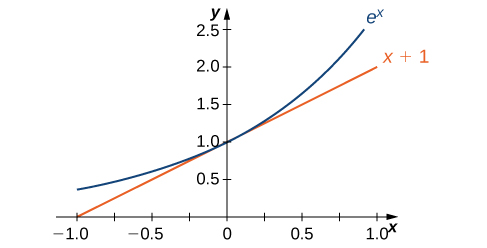
The graph of $E(x)=e^x$ together with the line $y=x+1$ are shown in Figure 3.138. This line is tangent to the graph of $E(x)=e^x$ at $x=0.$

"Graph of the function ex along with its tangent at (0, 1), x + 1." — Figure 3.138. The tangent line to $E(x)=e^x$ at $x=0$ has slope 1.

Now that we have laid out our basic assumptions, we begin our investigation by exploring the derivative of $B(x)=b^x,b\gt 0.$ Recall that we have assumed that $B'(0)$ exists. By applying the limit definition to the derivative we conclude that

\begin{equation*} B'(0)=\lim_{h\to 0}\frac{b^{0+h}- b^0}{h}=\lim_{h\to 0}\frac{b^h- 1}{h}. \end{equation*}

Turning to $B'(x),$ we obtain the following.

\begin{align*} B'(x)\amp=\lim_{h\to 0}\frac{b^{x+h}- b^x}{h}\amp \amp \text{ Apply the limit definition of the derivative. }\\ \amp=\lim_{h\to 0}\frac{b^xb^h- b^x}{h}\amp\amp\text{ Note that } b^{x+h}=b^xb^h.\\ \amp=\lim_{h\to 0}\frac{b^x(b^h- 1)}{h}\amp\amp\text{ Factor out } b^x.\\ \amp=b^x\lim_{h\to 0}\frac{b^h- 1}{h}\amp\amp\text{ Apply a property of limits. }\\ \amp=b^xB'(0)\amp\amp\text{ Use } B'(0)=\lim_{h\to 0}\frac{b^{0+h}- b^0}{h}=\lim_{h\to 0}\frac{b^h- 1}{h}. \end{align*}

We see that on the basis of the assumption that $B(x)=b^x$ is differentiable at $0,B(x)$ is not only differentiable everywhere, but its derivative is

\begin{equation*} B'(x)=b^xB'(0). \end{equation*}

For $E(x)=e^x,E'(0)=1.$ Thus, we have $E'(x)=e^x.$ (The value of $B'(0)$ for an arbitrary function of the form $B(x)=b^x,b\gt 0,$ will be derived later.)

Theorem 3.139. Derivative of the Natural Exponential Function.

Let $E(x)=e^x$ be the natural exponential function. Then

\begin{equation*} E'(x)=e^x. \end{equation*}

In general,

\begin{equation*} \frac{d}{dx}(e^{g(x)})=e^{g(x)}g'(x). \end{equation*}

Example 3.140. Derivative of an Exponential Function.

Find the derivative of $f(x)=e^{2x^2+x}.$

Solution.

Using the derivative formula and the chain rule,

\begin{align*} f'(x)\amp=e^{2x^2+x}\frac{d}{dx}(2x^2+x)\\ \amp=e^{2x^2+x}\cdot(4x+1). \end{align*}

Example 3.141. Combining Differentiation Rules.

Find the derivative of $y=\frac{e^{x^2}}{x}.$

Solution.

Use the derivative of the natural exponential function, the quotient rule, and the chain rule.

\begin{align*} y'\amp=\frac{(e^{x^2}\cdot 2)x\cdot x- 1\cdot e^{x^2}}{x^2}\amp \amp\text{ Apply the quotient rule. }\\ \amp =\frac{e^{x^2}(2x^2- 1)}{x^2}\amp \amp\text{ Simplify. } \end{align*}

Checkpoint 3.142.

Find the derivative of $h(x)=xe^{2x}.$

Hint.

Don’t forget to use the product rule.

Solution.

$h'(x)=e^{2x}+2xe^{2x}$

Example 3.143. Applying the Natural Exponential Function.

A colony of mosquitoes has an initial population of 1000. After $t$ days, the population is given by $A(t)=1000e^{0.3t}.$ Show that the ratio of the rate of change of the population, $A'(t),$ to the population, $A(t)$ is constant.

Solution.

First find $A'(t).$ By using the chain rule, we have $A'(t)=300e^{0.3t}.$ Thus, the ratio of the rate of change of the population to the population is given by

\begin{equation*} A'(t)=\frac{300e^{0.3t}}{1000e^{0.3t}}=0.3. \end{equation*}

The ratio of the rate of change of the population to the population is the constant 0.3.

Checkpoint 3.144.

If $A(t)=1000e^{0.3t}$ describes the mosquito population after $t$ days, as in the preceding example, what is the rate of change of $A(t)$ after 4 days?

Hint.

Find $A'(4).$

Solution.

996

Example 3.145. Applying the Natural Exponential Function to an Account with Interest Compounded Continuously.

If $A(t)=2500e^{0.012t}$ is the future value of an account in dollars with interest compounded continuously after $t$ years, what is the rate of change of $A(t)$ after 4 years?

Solution.

First find $A'(t).$ By using the chain rule, we have $A'(t)=2500e^{0.012t}\cdot 0.012=30e^{0.012t}.$ Thus, the rate of change of the future value of the account after 4 years is given by

\begin{equation*} A'(4)=30e^{0.012(4)}\approx \$31.48. \end{equation*}

Subsection 3.9.2 Derivative of the Logarithmic Function

Now that we have the derivative of the natural exponential function, we can use implicit differentiation to find the derivative of its inverse, the natural logarithmic function.

Theorem 3.146. The Derivative of the Natural Logarithmic Function.

If $x\gt 0$ and $y=\ln x,$ then

\begin{equation*} \frac{dy}{dx}=\frac{1}{x}. \end{equation*}

More generally, let $g(x)$ be a differentiable function. For all values of $x$ for which $g'(x)\gt 0,$ the derivative of $h(x)=\ln (g(x))$ is given by

\begin{equation*} h'(x)=\frac{1}{g(x)}g'(x). \end{equation*}

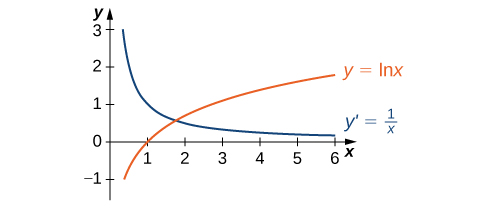
The graph of $y=\ln x$ and its derivative $\frac{dy}{dx}=\frac{1}{x}$ are shown in Figure 3.147.

"Graph of the function ln x along with its derivative 1/x. The function ln x is increasing on (0, + \infty ). Its derivative is decreasing but greater than 0 on (0, + \infty )." — Figure 3.147. $\text{ The function } y=\ln x$ is increasing on $(0,\text{ + }\infty ).$ Its derivative $y'=\frac{1}{x}$ is greater than zero on $(0,\text{ + }\infty ).$

Example 3.148. Taking a Derivative of a Natural Logarithm.

Find the derivative of $f(x)=\ln (x^3+3x- 4).$

Solution.

Use Equation directly.

\begin{align*} f'(x)\amp=\frac{1}{x^3+3x- 4}\cdot (3x^2+3)\amp\amp\text{ Use } g(x)=x^3+3x- 4 \text{ in } h'(x)=\frac{1}{g(x)}g'(x).\\ \amp=\frac{3x^2+3}{x^3+3x- 4}\amp\amp\text{ Rewrite. } \end{align*}

Example 3.149. Using Properties of Logarithms in a Derivative.

Find the derivative of $f(x)=\ln \left(\frac{x^2e^x}{5x+1}\right).$

Solution.

At first glance, taking this derivative appears rather complicated. However, by using the properties of logarithms prior to finding the derivative, we can make the problem much simpler. Applying properties of logarithms and then differentiating,

\begin{align*} f(x)\amp=\ln \left(\frac{x^2e^x}{5x+1}\right)=\ln (x^2e^x)-\ln (5x+1)\\ \amp=2\ln x+\ln e^x-\ln(5x+1)\\ \amp=2\ln x+x-\ln(5x+1)\\ f'(x)\amp=\frac{2}{x}+1-\frac{5}{5x+1}\amp\amp\text{ Apply sum rule and } h'(x)=\frac{1}{g(x)}g'(x). \end{align*}

Checkpoint 3.150.

Differentiate: $f(x)=\ln\left((3x+2)^5\right).$

Hint.

Use a property of logarithms to simplify before taking the derivative.

Solution.

$f'(x)=\frac{15}{3x+2}$

Now that we can differentiate the natural logarithmic function, we can use this result to find the derivatives of $y=log_bx$ and $y=b^x$ for $b\gt 0,b\neq 1.$

Theorem 3.151. Derivatives of General Exponential and Logarithmic Functions.

Let $b\gt 0,b\neq 1,$ and let $g(x)$ be a differentiable function.

If, $y=\log_bx,$ then
\begin{equation} \frac{dy}{dx}=\frac{1}{x \ln b}.\tag{3.9.1} \end{equation}
More generally, if $h(x)=\log_b(g(x)),$ then for all values of $x$ for which $g(x)\gt 0,$
\begin{equation} h'(x)=\frac{g'(x)}{g(x) \ln b}.\tag{3.9.2} \end{equation}
If $y=b^x,$ then
\begin{equation} \frac{dy}{dx}=b^x\ln b.\tag{3.9.3} \end{equation}
More generally, if $h(x)=b^{g(x)},$ then
\begin{equation} h'(x)=b^{g(x)}g\text{ ' }(x) \ln b.\tag{3.9.4} \end{equation}

Example 3.152. Applying Derivative Formulas.

Find the derivative of $h(x)=\frac{3^x}{3^x+2}.$

Solution.

Use the quotient rule and Theorem 3.151.

\begin{align*} h'(x)\amp=\frac{3^x \ln 3(3^x+2)- 3^x \ln 3(3^x)}{(3^x+2)^2}\amp\amp\text{ Apply the quotient rule. }\\ \amp=\frac{2\cdot 3^x \ln 3}{(3^x+2)^2}\amp\amp\text{ Simplify. } \end{align*}

Example 3.153.

Find the slope of the line tangent to the graph of $y=\log_{2} (3x+1)$ at $x=1.$

Solution.

To find the slope, we must evaluate $\frac{dy}{dx}$ at $x=1.$ Using (3.9.2), we see that

\begin{equation*} \frac{dy}{dx}=\frac{3}{ \ln 2(3x+1)}. \end{equation*}

By evaluating the derivative at $x=1,$ we see that the tangent line has slope

\begin{equation*} \frac{dy}{dx}\Bigg|_{x=1}=\frac{3}{4 \ln 2}=\frac{3}{ \ln 16}. \end{equation*}

Checkpoint 3.154.

Find the slope for the line tangent to $y=3^x$ at $x=2.$

Hint.

Evaluate the derivative at $x=2.$

Solution.

$9 \ln (3)$

Subsection 3.9.3 Key Concepts

On the basis of the assumption that the exponential function $y=b^x,b\gt 0$ is continuous everywhere and differentiable at 0, this function is differentiable everywhere and there is a formula for its derivative.
We can use a formula to find the derivative of $y=\ln x,$ and the relationship $\log_bx=\frac{\ln x}{\ln b}$ allows us to extend our differentiation formulas to include logarithms with arbitrary bases.

Subsection 3.9.4 Key Equations

Derivative of the natural exponential function $\frac{d}{dx}(e^{g(x)})=e^{g(x)}g'(x)$
Derivative of the natural logarithmic function $\frac{d}{dx}(\ln g(x))=\frac{1}{g(x)}g'(x)$
Derivative of the general exponential function $\frac{d}{dx}(b^{g(x)})=b^{g(x)}g'(x) \ln b$
Derivative of the general logarithmic function $\frac{d}{dx}(\log_bg(x))=\frac{g'(x)}{g(x) \ln b}$

This book is a custom edition based on OpenStax Calculus Volume 1. You can download the original for free at https://openstax.org/details/books/calculus-volume-1.