Skip to main content

Section 3.7 Derivatives of Inverse Functions

Learning Objectives.

  • Calculate the derivative of an inverse function.

  • Recognize the derivatives of the standard inverse trigonometric functions.

In this section we explore the relationship between the derivative of a function and the derivative of its inverse. For functions whose derivatives we already know, we can use this relationship to find derivatives of inverses without having to use the limit definition of the derivative. In particular, we will apply the formula for derivatives of inverse functions to trigonometric functions. This formula may also be used to extend the power rule to rational exponents.

Subsection 3.7.1 The Derivative of an Inverse Function

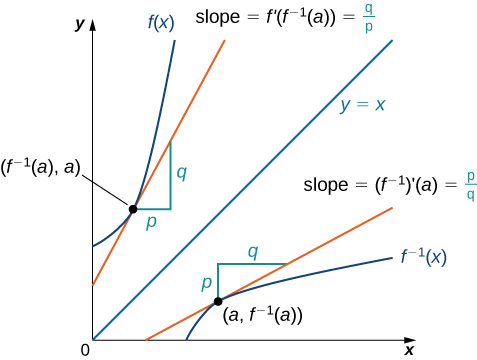
We begin by considering a function and its inverse. If \(f(x)\) is both invertible and differentiable, it seems reasonable that the inverse of \(f(x)\) is also differentiable. Figure 3.118 shows the relationship between a function \(f(x)\) and its inverse \(f^{-1}(x).\) Look at the point \((a,f^{-1}(a))\) on the graph of \(f^{-1}(x)\) having a tangent line with a slope of \({f^{-1}}'(a)=\frac{p}{q}.\) This point corresponds to a point \((f^{-1}(a),a)\) on the graph of \(f(x)\) having a tangent line with a slope of \(f'(f^{-1}(a))=\frac{q}{p}.\) Thus, if \(f^{-1}(x)\) is differentiable at \(a,\) then it must be the case that

\begin{equation*} {f^{-1}}'(a)=\frac{1}{f'(f^{-1}(a))}. \end{equation*}
"This graph shows a function f(x) and its inverse f−1(x). These functions are symmetric about the line y = x. The tangent line of the function f(x) at the point (f−1(a), a) and the tangent line of the function f−1(x) at (a, f−1(a)) are also symmetric about the line y = x. Specifically, if the slope of one were p/q, then the slope of the other would be q/p. Lastly, their derivatives are also symmetric about the line y = x."
Figure 3.118. The tangent lines of a function and its inverse are related; so, too, are the derivatives of these functions.

We may also derive the formula for the derivative of the inverse by first recalling that \(x=f(f^{-1}(x)).\) Then by differentiating both sides of this equation (using the chain rule on the right), we obtain

\begin{equation*} 1=f'(f^{-1}(x))({f^{-1}}'(x)). \end{equation*}

Solving for \({f^{-1}}'(x),\) we obtain

\begin{equation*} {f^{-1}}'(x)=\frac{1}{f'(f^{-1}(x))}. \end{equation*}

We summarize this result in the following theorem.

Example 3.120. Applying the Inverse Function Theorem.

Use the inverse function theorem to find the derivative of \(g(x)=\frac{x+2}{x}.\) Compare the resulting derivative to that obtained by differentiating the function directly.

Solution.

The inverse of \(g(x)=\frac{x+2}{x}\) is \(f(x)=\frac{2}{x−1}.\) Since \(g'(x)=\frac{1}{f'(g(x))},\) begin by finding \(f'(x).\) Thus,

\begin{equation*} f'(x)=\frac{−2}{(x-1)^2} \text{ and } f'(g(x))=\frac{−2}{(g(x)−1)^2}=\frac{−2}{(\frac{x+2}{x}−1)^2}=−\frac{x^2}{2}. \end{equation*}

Finally,

\begin{equation*} g'(x)=\frac{1}{f'(g(x))}=−\frac{2}{x^2}. \end{equation*}

We can verify that this is the correct derivative by applying the quotient rule to \(g(x)\) to obtain

\begin{equation*} g'(x)=−\frac{2}{x^2}. \end{equation*}

Checkpoint 3.121.

Use the inverse function theorem to find the derivative of \(g(x)=\frac{1}{x+2}.\) Compare the result obtained by differentiating \(g(x)\) directly.

Hint.

Use the preceding example as a guide.

Solution.

\(g'(x)=−\frac{1}{(x+2)^2}\)

Example 3.122. Applying the Inverse Function Theorem.

Use the inverse function theorem to find the derivative of \(g(x)=\sqrt[3]{x}.\)

Solution.

The function \(g(x)=\sqrt[3]{x}\) is the inverse of the function \(f(x)=x^3.\) Since \(g'(x)=\frac{1}{f'(g(x))},\) begin by finding \(f'(x).\) Thus,

\begin{equation*} f'(x)=3x^3 \text{ and } f'(g(x))=3(\sqrt[3]{x})^2=3x2/^3. \end{equation*}

Finally,

\begin{equation*} g'(x)=\frac{1}{3x^{2/3}}=\frac{1}{3}x^{−2/3}. \end{equation*}

Checkpoint 3.123.

Find the derivative of \(g(x)=\sqrt[5]{x}\) by applying the inverse function theorem.

Hint.

\(g(x)\) is the inverse of \(f(x)=x^5.\)

Solution.

\(g(x)=\frac{1}{5}x^{-4/5}\)

From the previous example, we see that we can use the inverse function theorem to extend the power rule to exponents of the form \(\frac{1}{n},\) where \(n\) is a positive integer. This extension will ultimately allow us to differentiate \(x^q,\) where \(q\) is any rational number.

The function \(g(x)=x^{1/n}\) is the inverse of the function \(f(x)=x^n.\) Since \(g'(x)=\frac{1}{f'(g(x))},\) begin by finding \(f'(x).\) Thus,

\begin{equation*} f'(x)=nx^{n-1} \text{ and } f'(g(x))=n(x^{1/n})^{n−1}=nx^{(n−1)/n}. \end{equation*}

Finally,

\begin{equation*} g'(x)=\frac{1}{nx^{(n−1)/n}}=\frac{1}{n}x^{(1−n)/n}=\frac{1}{n}x^{(1/n)−1}. \end{equation*}

To differentiate \(x^{m/n}\) we must rewrite it as \((x^{1/n})^m\) and apply the chain rule. Thus,

\begin{equation*} \frac{d}{dx}(x^{m/n})=\frac{d}{dx}((x^{1/n})^m)=m(x^{1/n})^{m−1}\cdot \frac{1}{n}x^{(1/n)−1}=\frac{m}{n}x^{(m/n)−1}. \end{equation*}

Example 3.125. Applying the Power Rule to a Rational Power.

Find the equation of the line tangent to the graph of \(y=x^{2/3}\) at \(x=8.\)

Solution.

First find \(\frac{dy}{dx}\) and evaluate it at \(x=8.\) Since

\begin{equation*} \frac{dy}{dx}=\frac{2}{3}x^{−1/3} \text{ and } \frac{dy}{dx}|_{x=8}=\frac{1}{3} \end{equation*}

the slope of the tangent line to the graph at \(x=8\) is \(\frac{1}{3}.\)

Substituting \(x=8\) into the original function, we obtain \(y=4.\) Thus, the tangent line passes through the point \((8,4).\) Substituting into the point-slope formula for a line, we obtain the tangent line

\begin{equation*} y=\frac{1}{3}x+\frac{4}{3}. \end{equation*}

Checkpoint 3.126.

Find the derivative of \(s(t)=\sqrt{2t+1}.\)

Hint.

Use the chain rule.

Solution.

\(s'(t)=(2t+1)^{-1/2}\)

Subsection 3.7.2 Key Concepts

  • The inverse function theorem allows us to compute derivatives of inverse functions without using the limit definition of the derivative.

  • We can use the inverse function theorem to develop differentiation formulas for the inverse trigonometric functions.

Subsection 3.7.3 Key Equations

  • Inverse function theorem \({f^{-1}}'(x)=\frac{1}{f'(f^{-1}(x))}\) whenever \(f'(f^{-1}(x))\neq 0\) and \(f(x)\) is differentiable.

  • Power rule with rational exponents \(\frac{d}{dx}(x^{m/n})=\frac{m}{n}x^{(m/n)−1}.\)

This book is a custom edition based on OpenStax Calculus Volume 1. You can download the original for free at https://openstax.org/details/books/calculus-volume-1.