Skip to main content

Section 1.7 Exponential Functions

Learning Objectives.

  1. Identify the form of an exponential function.

  2. Explain the difference between the graphs of \(x^b\) and \(b^x.\)

  3. Recognize the significance of the number \(e.\)

In this section we examine exponential functions. We use the properties of these functions to solve equations involving exponential terms, and we study the meaning and importance of the number \(e\text{.}\) Note: This the first half of section 1.5 in the original version of OpenStax Calculus.

Subsection 1.7.1 Exponential Functions

Exponential functions arise in many applications. One common example is population growth.

For example, if a population starts with \(P_0\) individuals and then grows at an annual rate of \(2\%,\) its population after 1 year is

\begin{equation*} P(1)=P_0+0.02P_0=P_0(1+0.02)=P_0(1.02). \end{equation*}

Its population after 2 years is

\begin{equation*} P(2)=P(1)+0.02P(1)=P(1)(1.02)=P_0(1.02)^2. \end{equation*}

In general, its population after \(t\) years is

\begin{equation*} P(t)=P_0(1.02)^t, \end{equation*}

which is an exponential function. More generally, any function of the form \(f(x)=b^x,\) where \(b\gt 0,b\neq 1,\) is an exponential function with base \(b\) and exponent \(x\text{.}\) Exponential functions have constant bases and variable exponents. Note that a function of the form \(f(x)=x^b\) for some constant \(b\) is not an exponential function but a power function.

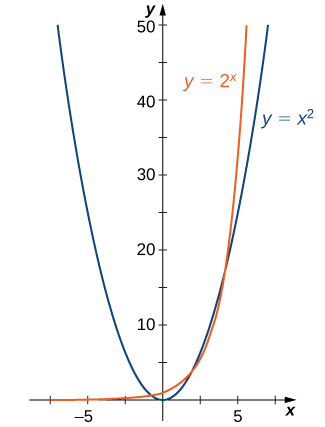
To see the difference between an exponential function and a power function, we compare the functions \(y=x^2\) and \(y=2^x.\) In Table 1.107, we see that both \(2^x\) and \(x^2\) approach infinity as \(x\to \infty.\) Eventually, however, \(2^x\) becomes larger than \(x^2\) and grows more rapidly as \(x\to \infty.\) In the opposite direction, as \(x\to -\infty,x^2\to \infty,\) whereas \(2^x\to 0.\) The line \(y=0\) is a horizontal asymptote for \(y=2^x.\)

Table 1.107. Values of \(x^2\) and \(2^x\)
\(x\) \(−3\) \(−2\) \(−1\) \(0\) \(1\) \(2\) \(3\) \(4\) \(5\) \(6\)
\(x^2\) \(9\) \(4\) \(1\) \(0\) \(1\) \(4\) \(9\) \(16\) \(25\) \(36\)
\(2^x\) \(1/8\) \(1/4\) \(1/2\) \(1\) \(2\) \(4\) \(8\) \(16\) \(32\) \(64\)

In Figure 1.108, we graph both \(y=x^2\) and \(y=2^x\) to show how the graphs differ.

"An image of a graph. The x axis runs from -10 to 10 and the y axis runs from 0 to 50. The graph is of two functions. The first function is “y = x squared”, which is a parabola. The function decreases until it hits the origin and then begins increasing. The second function is “y = 2 to the power of x”, which starts slightly above the x axis, and begins increasing very rapidly, more rapidly than the first function."
Figure 1.108. Both \(2^x\) and \(x^2\) approach infinity as \(x\to \infty,\) but \(2^x\) grows more rapidly than \(x^2.\) As \(x\to -\infty,x^2\to \infty,\) whereas \(2^x\to 0.\)

Subsubsection 1.7.1.1 Evaluating Exponential Functions

Recall the properties of exponents: If \(x\) is a positive integer, then we define \(b^x=b\cdot b\cdots b\) (with \(x\) factors of \(b).\) If \(x\) is a negative integer, then \(x=.y\) for some positive integer \(y,\) and we define \(b^x=b^{-y}=1/b^y.\) Also, \(b^0\) is defined to be \(1.\) If \(x\) is a rational number, then \(x=p/q,\) where \(p\) and \(q\) are integers and \(b^x=b^{p/q}=\sqrt[q]{b^p}.\) For example, \(9^{3/2}=\sqrt{9^3}=27.\) However, how is \(b^x\) defined if \(x\) is an irrational number? For example, what do we mean by \(2^\sqrt{2}\) This is too complex a question for us to answer fully right now; however, we can make an approximation. In Table 1.109, we list some rational numbers approaching \(\sqrt{2},\) and the values of \(2^x\) for each rational number \(x\) are presented as well. We claim that if we choose rational numbers \(x\) getting closer and closer to \(\sqrt{2},\) the values of \(2^x\) get closer and closer to some number \(L.\) We define that number \(L\) to be \(2^\sqrt{2}.\)

Table 1.109. Values of \(2^x\) for a List of Rational Numbers Approximating \(\sqrt{2}\)
\(x\) \(1.4\) \(1.41\) \(1.414\) \(1.4142\) \(1.41421\) \(1.414213\)
\(2^x\) \(2.639\) \(2.65737\) \(2.66475\) \(2.665119\) \(2.665138\) \(2.665143\)
Example 1.110. Bacterial Growth.

Suppose a particular population of bacteria is known to double in size every \(4\) hours. If a culture starts with \(1000\) bacteria, the number of bacteria after \(4\) hours is \(n(4)=1000\cdot 2.\) The number of bacteria after \(8\) hours is \(n(8)=n(4)\cdot 2=1000\cdot 2^2.\) In general, the number of bacteria after \(4m\) hours is \(n(4m)=1000\cdot 2^m.\) Letting \(t=4m,\) we see that the number of bacteria after \(t\) hours is \(n(t)=1000\cdot 2^{t/4}.\) Find the number of bacteria after \(6\) hours, \(10\) hours, and \(24\) hours.

Solution.

The number of bacteria after 6 hours is given by \(n(6)=1000\cdot 2^{6/4} \approx 2828\) bacteria. The number of bacteria after \(10\) hours is given by \(n(10)=1000\cdot 2^{10/4}≈5657\) bacteria. The number of bacteria after \(24\) hours is given by \(n(24)=1000\cdot 2^6=64,000\) bacteria.

Checkpoint 1.111.

Given the exponential function \(f(x)=100\cdot 3^{x/2},\) evaluate \(f(4)\) and \(f(10).\)

Solution.

\(f(4)=900;f(10)=24,300.\)

Subsubsection 1.7.1.2 Graphing Exponential Functions

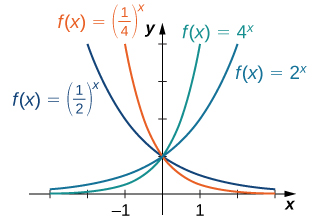
For any base \(b\gt 0,b\neq 1,\) the exponential function \(f(x)=b^x\) is defined for all real numbers \(x\) and \(b^x\gt 0.\) Therefore, the domain of \(f(x)=b^x\) is \((-\infty,\infty)\) and the range is \((0,\infty).\) To graph \(b^x,\) we note that for \(b\gt 1,b^x\) is increasing on \((-\infty,\infty)\) and \(b^x\to \infty\) as \(x\to \infty,\) whereas \(b^x\to 0\) as \(x\to -\infty.\) On the other hand, if \(0\lt b\lt 1,f(x)=b^x\) is decreasing on \((-\infty,\infty)\) and \(b^x\to 0\) as \(x\to \infty\) whereas \(b^x\to \infty\) as \(x\to -\infty\) (Figure 1.113).

"An image of a graph. The x axis runs from -3 to 3 and the y axis runs from 0 to 4. The graph is of four functions. The first function is “f(x) = 2 to the power of x”, an increasing curved function, which starts slightly above the x axis and begins increasing. The second function is “f(x) = 4 to the power of x”, an increasing curved function, which starts slightly above the x axis and begins increasing rapidly, more rapidly than the first function. The third function is “f(x) = (1/2) to the power of x”, a decreasing curved function with decreases until it gets close to the x axis without touching it. The third function is “f(x) = (1/4) to the power of x”, a decreasing curved function with decreases until it gets close to the x axis without touching it. It decreases at a faster rate than the third function."
Figure 1.113. If \(b\gt 1,\) then \(b^x\) is increasing on \((-\infty,\infty).\) If \(0\lt b\lt 1,\) then \(b^x\) is decreasing on \((-\infty,\infty).\)
Note 1.114. Media.

Visit this site 2  for more exploration of the graphs of exponential functions.

Note that exponential functions satisfy the general laws of exponents. To remind you of these laws, we state them as rules.

Note 1.115. Rule: Laws of Exponents.

For any constants \(a\gt 0,b\gt 0,\) and for all \(x\) and y,

  1. \(\displaystyle b^x\cdot b^y=b^{x+y}\)

  2. \(\displaystyle \frac{b^x}{b^y}=b^{x−y}\)

  3. \(\displaystyle (b^x)^y=b^{xy}\)

  4. \(\displaystyle (ab)^x=a^xb^x\)

  5. \(\displaystyle \frac{a^x}{b^x}=\left(\frac{a}{b}\right)^x\)

Example 1.116. Using the Laws of Exponents.

Use the laws of exponents to simplify each of the following expressions.

  1. \(\displaystyle \frac{(2x^{2/3})^3}{(4x^{−1/3})^2}\)

  2. \(\displaystyle \frac{(x^3y^{−1})^2}{(xy^2)^{−2}}\)

Solution.

  1. We can simplify as follows:

    \begin{equation*} \frac{(2x^{2/3})^3}{(4x^{−1/3})^2}= \frac{2^3(x^{2/3})^3}{4^2(x^{−1/3})^2}= \frac{8x^2}{16x^{−2/3}}= \frac{x^2x^{2/3}}{2}= \frac{x^{8/3}}{2}. \end{equation*}

  2. We can simplify as follows:

    \begin{equation*} \frac{(x^3y^{−1})^2}{(xy^2)^{−2}}=\frac{(x^3)^2(y^{−1})^2}{x^{−2}(y^2)^{−2}}= \frac{x^6y^{−2}}{x^{−2}y^{−4}}=x^6x^2y^{−2}y^4=x^8y^2. \end{equation*}

Checkpoint 1.117.

Use the laws of exponents to simplify \((6x^{−3}y^2)/(12x^{−4}y^5).\)

Hint.

\(x^a/x^b=x^{a−b}\)

Solution.

\(x/(2y^3)\)

Subsection 1.7.2 The Number \(e \)

A special type of exponential function appears frequently in real-world applications. To describe it, consider the following example of exponential growth, which arises from compounding interest in a savings account. Suppose a person invests \(P\) dollars in a savings account with an annual interest rate \(r,\) compounded annually. The amount of money after 1 year is

\begin{equation*} A(1)=P+rP=P(1+r). \end{equation*}

The amount of money after \(2\) years is

\begin{equation*} A(2)=A(1)+rA(1)=P(1+r)+rP(1+r)=P(1+r)^2. \end{equation*}

More generally, the amount after \(t\) years is

\begin{equation*} A(t)=P(1+r)^t. \end{equation*}

If the money is compounded 2 times per year, the amount of money after half a year is

\begin{equation*} A\left(\frac{1}{2}\right)=P+\left(\frac{r}{2}\right)P=P\left(1+\left(\frac{r}{2}\right)\right). \end{equation*}

The amount of money after \(1\) year is

\begin{equation*} A\left(1\right)=A\left(\frac{1}{2}\right)+\left(\frac{r}{2}\right)A\left(\frac{1}{2}\right)=P\left(1+\frac{r}{2}\right)+\frac{r}{2}\left(P\left(1+\frac{r}{2}\right)\right)=P\left(1+\frac{r}{2}\right)^2. \end{equation*}

After \(t\) years, the amount of money in the account is

\begin{equation*} A\left(t\right)=P\left(1+\frac{r}{2}\right)^{2t}. \end{equation*}

More generally, if the money is compounded \(n\) times per year, the amount of money in the account after \(t\) years is given by the function

\begin{equation*} A\left(t\right)=P\left(1+\frac{r}{n}\right)^{nt}. \end{equation*}

What happens as \(n\to \infty?\) To answer this question, we let \(m=n/r\) and write

\begin{equation*} \left(1+ \frac{r}{n}\right)^{nt}=\left(1+ \frac{1}{m}\right)^{mrt}, \end{equation*}

and examine the behavior of \(\left(1+1/m\right)^m\) as \(m\to \infty,\) using a table of values (Table 1.118).

Table 1.118. Values of \(\left(1+ \frac{1}{m}\right)^m\) as \(m\to \infty\)
\(m\) \(10\) \(100\) \(1000\) \(10,000\) \(100,000\) \(1,000,000\)
\(\left(1+ \frac{1}{m}\right)^m\) \(2.5937\) \(2.7048\) \(2.71692\) \(2.71815\) \(2.718268\) \(2.718280\)

Looking at this table, it appears that \((1+1/m)^m\) is approaching a number between \(2.7\) and \(2.8\) as \(m\to \infty.\) In fact, \((1+1/m)^m\) does approach some number as \(m\to \infty.\) We call this number \(e\). To six decimal places of accuracy,

\begin{equation*} e≈2.718282. \end{equation*}

The letter \(e\) was first used to represent this number by the Swiss mathematician Leonhard Euler during the 1720s. Although Euler did not discover the number, he showed many important connections between \(e\) and logarithmic functions. We still use the notation \(e\) today to honor Euler’s work because it appears in many areas of mathematics and because we can use it in many practical applications.

Returning to our savings account example, we can conclude that if a person puts \(P\) dollars in an account at an annual interest rate \(r,\) compounded continuously, then \(A(t)=Pe^{rt}.\) This function may be familiar. Since functions involving base \(e\) arise often in applications, we call the function \(f(x)=e^x\) the natural exponential function. Not only is this function interesting because of the definition of the number \(e,\) but also, as discussed next, its graph has an important property.

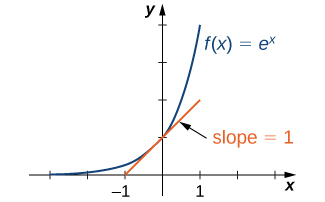
Since \(e\gt 1,\) we know \(e^x\) is increasing on \((-\infty,\infty).\) In Figure 1.119, we show a graph of \(f(x)=e^x\) along with a tangent line to the graph of at \(x=0.\) We give a precise definition of tangent line in the next chapter; but, informally, we say a tangent line to a graph of \(f\) at \(x=a\) is a line that passes through the point \((a,f(a))\) and has the same "slope" as \(f\) at that point \(.\) The function \(f(x)=e^x\) is the only exponential function \(b^x\) with tangent line at \(x=0\) that has a slope of 1. As we see later in the text, having this property makes the natural exponential function the most simple exponential function to use in many instances.

"An image of a graph. The x axis runs from -3 to 3 and the y axis runs from 0 to 4. The graph is of the function “f(x) = e to power of x”, an increasing curved function that starts slightly above the x axis. The y intercept is at the point (0, 1). At this point, a line is drawn tangent to the function. This line has the label “slope = 1”."
Figure 1.119. The graph of \(f(x)=e^x\) has a tangent line with slope \(1\) at \(x=0.\)

Example 1.120. Compounding Interest.

Suppose \(.500\) is invested in an account at an annual interest rate of \(r=5.5%,\) compounded continuously.

  1. Let \(t\) denote the number of years after the initial investment and \(A(t)\) denote the amount of money in the account at time \(t.\) Find a formula for \(A(t).\)

  2. Find the amount of money in the account after \(10\) years and after \(20\) years.

Solution.

  1. If \(P\) dollars are invested in an account at an annual interest rate \(r,\) compounded continuously, then \(A(t)=Pe^{rt}.\) Here \(P=.500\) and \(r=0.055.\) Therefore, \(A(t)=500e^{0.055t}.\)

  2. After \(10\) years, the amount of money in the account is

    \begin{equation*} A(10)=500e^{0.055\cdot 10}=500e^{0.55}≈866.63. \end{equation*}
    After \(20\) years, the amount of money in the account is
    \begin{equation*} A(20)=500e^{0.055\cdot 20}=500e^{1.1}≈1,502.08. \end{equation*}

Checkpoint 1.121.

If \(.750\) is invested in an account at an annual interest rate of \(4%,\) compounded continuously, find a formula for the amount of money in the account after \(t\) years. Find the amount of money after \(30\) years.

Hint.

\(A(t)=Pe^{rt}.\)

Solution.

\(A(t)=750e^{0.04t}.\) After \(30\) years, there will be approximately \(2,490.09.\)

Subsection 1.7.3 Key Concepts

  • The exponential function \(y=b^x\) is increasing if \(b\gt 1\) and decreasing if \(0\lt b\lt 1.\) Its domain is \((-\infty,\infty)\) and its range is \((0,\infty).\)

  • The natural exponential function is \(y=e^x\text{.}\)

This book is a custom edition based on OpenStax Calculus Volume 1. You can download the original for free at https://openstax.org/details/books/calculus-volume-1. 3 

Additional practice exercises are available in at the bottom on this section in OpenStax Calculus Volume 1: https://openstax.org/books/calculus-volume-1/pages/1-5-exponential-and-logarithmic-functions

openstax.org/l/20_exponengrow
openstax.org/1/20_inverse
https://openstax.org/details/books/calculus-volume-1