Section 1.3 Review of Functions: Part B
Learning Objectives.
Define when a function is increasing, decreasing, concave up and concave down.
Make new functions from two or more given functions.
Describe the symmetry properties of a function.
We will continue to discuss functions. We will define what it means for a function to be increasing, decreasing, concave up and concave down, look at symmetries of functions and see various ways to get new functions from given ones. This is a continuation of Review of Functions Part A. In the original OpenStax Calculus Book, it is the second half of section 1.1.
Subsection 1.3.1 Increasing and Decresing
In part A, we looked at the graph of \(f(x)=-4x+2 \) which is reproduced below.
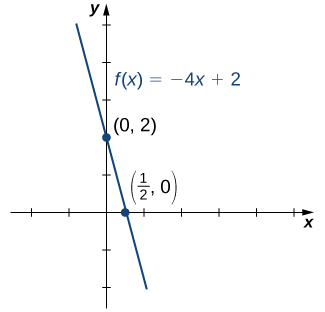
Note that for this function and the function \(f(x)=-4x+2\) graphed in Figure 1.34, the values of \(f(x)\) are getting smaller as \(x\) is getting larger. A function with this property is said to be decreasing. On the other hand, for the function \(f(x)=\sqrt{x+3}+1\) graphed in Figure 1.29, the values of \(f(x)\) are getting larger as the values of \(x\) are getting larger. A function with this property is said to be increasing. It is important to note, however, that a function can be increasing on some interval or intervals and decreasing over a different interval or intervals. For example, using our temperature function in Figure 1.21, we can see that the function is decreasing on the interval \((0,4),\) increasing on the interval \((4,14),\) and then decreasing on the interval \((14,23).\) We make the idea of a function increasing or decreasing over a particular interval more precise in the next definition.
Definition 1.35.
We say that a function \(f\) is increasing on the interval \(I\) if for all \(x_1,x_2\in I,\)
We say \(f\) is strictly increasing on the interval \(I\) if for all \(x_1,x_2\in I,\)
We say that a function \(f\) is decreasing on the interval \(I\) if for all \(x_1,x_2\in I,\)
We say that a function \(f\) is strictly decreasing on the interval \(I\) if for all \(x_1,x_2\in I,\)
For example, the function \(f(x)=3x\) is increasing on the interval \((-\infty, \infty)\) because \(3x_1 < 3x_2\) whenever \(x_1 < x_2.\) On the other hand, the function \(f(x)=-x^3\) is decreasing on the interval \((-\infty, \infty)\) because \(-(x_1)^3 > -(x_2)^3\) whenever \(x_1 < x_2\) (Figure 1.36).
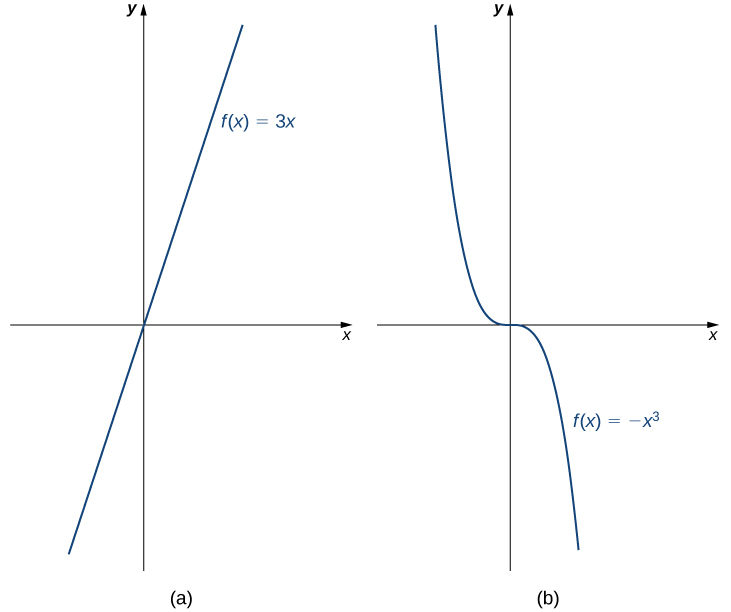
Definition 1.37.
We say that a function \(f\) is concave up on the interval \(I\) if the graph bends upwards on \(I\text{.}\)
We say that a function \(f\) is concave down on the interval \(I\) if the graph bends downwards on \(I\text{.}\)
For example, the function \(f(x)=x^2+1\) is concave up on the entire real line, that is, on the interval \((-\infty,\infty)\) since the graph of \(f\) bends upwards. Notice that a function may not be concave up/concave down everywhere. It may change concavity. This is illustrated in the following example.
Observe that \(g(x)=x^3\) is concave down on the interval \((-\infty,0)\) since the graph of \(g\) bends upwards on this interval. Moreover, \(g\) is concave up on the interval \((0,\infty)\) since the graph of \(g\) bends downwards on this interval.
Subsection 1.3.2 Combining Functions
Now that we have reviewed the basic characteristics of functions, we can see what happens to these properties when we combine functions in different ways, using basic mathematical operations to create new functions. For example, if the cost for a company to manufacture \(x\) items is described by the function \(C(x)\) and the revenue created by the sale of \(x\) items is described by the function \(R(x),\) then the profit on the manufacture and sale of \(x\) items is defined as \(P(x)=R(x)-C(x).\) Using the difference between two functions, we created a new function.
Alternatively, we can create a new function by composing two functions. For example, given the functions \(f(x)=x^2\) and \(g(x)=3x+1,\) the composite function \(f\circ g\) is defined such that
The composite function \(g\circ f\) is defined such that
Note that these two new functions are different from each other.
Subsubsection 1.3.2.1 Combining Functions with Mathematical Operators
To combine functions using mathematical operators, we simply write the functions with the operator and simplify. Given two functions \(f\) and \(g,\) we can define four new functions:
Example 1.38. Combining Functions Using Mathematical Operations.
Given the functions \(f(x)=2x-3\) and \(g(x)=x^2-1,\) find each of the following functions and state its domain.
\(\displaystyle (f+g)(x)\)
\(\displaystyle (f-g)(x)\)
\(\displaystyle (f·g)(x)\)
\(\displaystyle \left(\frac{f}{g}\right)(x)\)
\((f+g)(x)=(2x-3)+(x^2-1)=x^2+2x-4.\) The domain of this function is the interval \((-\infty,\infty).\)
\((f-g)(x)=(2x-3)-(x^2-1)=-x^2+2x-2.\) The domain of this function is the interval \((-\infty,\infty).\)
\((f·g)(x)=(2x-3)(x^2-1)=2x^3-3x^2-2x+3.\) The domain of this function is the interval \((-\infty,\infty).\)
\(\left(\frac{f}{g}\right)(x)=\frac{2x-3}{x^2-1}.\) The domain of this function is \(\{x|x\neq\pm 1\}.\)
Checkpoint 1.39.
For \(f(x)=x^2+3\) and \(g(x)=2x-5,\) find \(\left(f/g\right)(x)\) and state its domain.
Subsubsection 1.3.2.2 Function Composition
When we compose functions, we take a function of a function. For example, suppose the temperature \(T\) on a given day is described as a function of time \(t\) (measured in hours after midnight) as in Table 1.20. Suppose the cost \(C,\) to heat or cool a building for 1 hour, can be described as a function of the temperature \(T.\) Combining these two functions, we can describe the cost of heating or cooling a building as a function of time by evaluating \(C(T(t)).\) We have defined a new function, denoted \(C\circ T,\) which is defined such that \((C\circ T)(t)=C(T(t))\) for all \(t\) in the domain of \(T.\) This new function is called a composite function. We note that since cost is a function of temperature and temperature is a function of time, it makes sense to define this new function \((C\circ T)(t).\) It does not make sense to consider \((T\circ C)(t),\) because temperature is not a function of cost.
Definition 1.40.
Consider the function \(f\) with domain \(A\) and range \(B,\) and the function \(g\) with domain \(D\) and range \(E.\) If \(B\) is a subset of \(D,\) then the composite function \((g\circ f)(x)\) is the function with domain \(A\) such that
A composite function \(g\circ f\) can be viewed in two steps. First, the function \(f\) maps each input \(x\) in the domain of \(f\) to its output \(f(x)\) in the range of \(f.\) Second, since the range of \(f\) is a subset of the domain of \(g,\) the output \(f(x)\) is an element in the domain of \(g,\) and therefore it is mapped to an output \(g(f(x))\) in the range of \(g.\) In Figure 1.41, we see a visual image of a composite function.
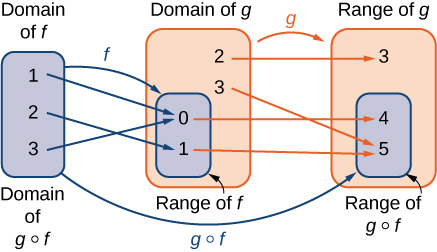
Example 1.42. Compositions of Functions Defined by Formulas.
Consider the functions \(f(x)=x^2+1\) and \(g(x)=1/x.\)
Find \((g\circ f)(x)\) and state its domain and range.
Evaluate \((g\circ f)(4),(g\circ f)(-1/2).\)
Find \((f\circ g)(x)\) and state its domain and range.
Evaluate \((f\circ g)(4),(f\circ g)(-1/2).\)
We can find the formula for \((g\circ f)(x)\) in two different ways. We could write
\begin{equation*} (g\circ f)(x)=g(f(x))=g(x^2+1)=\frac{1}{x^2+1}. \end{equation*}Alternatively, we could write\begin{equation*} (g\circ f)(x)=g(f(x))=\frac{1}{f(x)}=\frac{1}{x^2+1}. \end{equation*}Since \(x^2+1\neq 0\) for all real numbers \(x,\) the domain of \((g\circ f)(x)\) is the set of all real numbers. Since \(0 \lt 1/(x^2+1) \leq 1,\) the range is, at most, the interval \((0,1].\) To show that the range is this entire interval, we let \(y=1/(x^2+1)\) and solve this equation for \(x\) to show that for all \(y\) in the interval \((0,1],\) there exists a real number \(x\) such that \(y=1/(x^2+1).\) Solving this equation for \(x,\) we see that \(x^2+1=1/y,\) which implies that\begin{equation*} x=\pm\sqrt{\frac{1}{y}-1}. \end{equation*}If \(y\) is in the interval \((0,1],\) the expression under the radical is nonnegative, and therefore there exists a real number \(x\) such that \(1/(x^2+1)=y.\) We conclude that the range of \(g\circ f\) is the interval \((0,1].\)\((g\circ f)(4)=g(f(4))=g(4^2+1)=g(17)=\frac{1}{17}\) and \((g\circ f)(-\frac{1}{2})=g(f(-\frac{1}{2}))=g((-\frac{1}{2})^2+1)=g(\frac{5}{4})=\frac{4}{5}\)
We can find a formula for \((f\circ g)(x)\) in two ways. First, we could write
\begin{equation*} (f\circ g)(x)=f(g(x))=f\left(\frac{1}{x}\right)=\left(\frac{1}{x}\right)^2+1. \end{equation*}Alternatively, we could write\begin{equation*} (f\circ g)(x)=f(g(x))=(g(x))^2+1=\left(\frac{1}{x}\right)^2+1. \end{equation*}The domain of \(f\circ g\) is the set of all real numbers \(x\) such that \(x\neq 0.\) To find the range of \(f,\) we need to find all values \(y\) for which there exists a real number \(x\neq0\) such that\begin{equation*} \left(\frac{1}{x}\right)^2+1=y. \end{equation*}Solving this equation for \(x,\) we see that we need \(x\) to satisfy\begin{equation*} \left(\frac{1}{x}\right)^2=y-1, \end{equation*}which simplifies to\begin{equation*} \frac{1}{x}=\pm\sqrt{y-1}. \end{equation*}Finally, we obtain\begin{equation*} x=\pm\frac{1}{\sqrt{y-1}}. \end{equation*}Since \(1/\sqrt{y-1}\) is a real number if and only if \(y\gt 1,\) the range of \(f\) is the set \(\{y|y\gt 1\}.\)\((f\circ g)(4)=f(g(4))=f(\frac{1}{4})=(\frac{1}{4})^2+1=\frac{17}{16}\) \((f\circ g)(-\frac{1}{2})=f(g(-\frac{1}{2}))=f(-2)=(-2)^2+1=5\)
In Example 1.42, we can see that \((f\circ g)(x)\neq(g\circ f)(x).\) This tells us, in general terms, that the order in which we compose functions matters.
Checkpoint 1.43.
Let \(f(x)=2-5x.\) Let \(g(x)=\sqrt{x}.\) Find \((f\circ g)(x).\)
\((f\circ g)(x)=2-5\sqrt{x}.\)
Example 1.44. Composition of Functions Defined by Tables.
Test
Consider the functions \(f\) and \(g\) described by Table 1.45 and Table 1.46.
| \(x\) | \(-3\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) |
| \(f(x)\) | \(0\) | \(4\) | \(2\) | \(4\) | \(-2\) | \(0\) | \(-2\) | \(4\) |
| \(x\) | \(-4\) | \(-2\) | \(0\) | \(2\) | \(4\) |
| \(g(x)\) | \(1\) | \(0\) | \(3\) | \(0\) | \(5\) |
Evaluate \((g\circ f)(3),(g\circ f)(0).\)
State the domain and range of \((g\circ f)(x).\)
Evaluate \((f\circ f)(3),(f\circ f)(1).\)
State the domain and range of \((f\circ f)(x).\)
\((g\circ f)(3)=g(f(3))=g(-2)=0\) \((g\circ f)(0)=g(4)=5\)
The domain of \(g\circ f\) is the set \(\{-3,-2,-1,0,1,2,3,4\}.\) Since the range of \(f\) is the set \(\{-2,0,2,4\},\) the range of \(g\circ f\) is the set \({0,3,5}.\)
\((f\circ f)(3)=f(f(3))=f(-2)=4\) \((f\circ f)(1)=f(f(1))=f(-2)=4\)
The domain of \(f\circ f\) is the set \(\{-3,-2,-1,0,1,2,3,4\}.\) Since the range of \(f\) is the set \(\{-2,0,2,4\},\) the range of \(f\circ f\) is the set \(\{0,4\}.\)
Example 1.47. Application Involving a Composite Function.
A store is advertising a sale of \(20\%\) off all merchandise. Caroline has a coupon that entitles her to an additional \(15\%\) off any item, including sale merchandise. If Caroline decides to purchase an item with an original price of \(x\) dollars, how much will she end up paying if she applies her coupon to the sale price? Solve this problem by using a composite function.
Since the sale price is \(20\%\) off the original price, if an item is \(x\) dollars, its sale price is given by \(f(x)=0.80x.\) Since the coupon entitles an individual to \(15\%\) off the price of any item, if an item is \(y\) dollars, the price, after applying the coupon, is given by \(g(y)=0.85y.\) Therefore, if the price is originally \(x\) dollars, its sale price will be \(f(x)=0.80x\) and then its final price after the coupon will be \(g(f(x))=0.85(0.80x)=0.68x.\)
Checkpoint 1.48.
If items are on sale for \(10\%\) off their original price, and a customer has a coupon for an additional \(30\%\) off, what will be the final price for an item that is originally \(x\) dollars, after applying the coupon to the sale price?
Subsection 1.3.3 Symmetry of Functions
The graphs of certain functions have symmetry properties that help us understand the function and the shape of its graph. For example, consider the function \(f(x)=x^4-2x^2-3\) shown in Figure 1.49(a). If we take the part of the curve that lies to the right of the \(y\)-axis and flip it over the \(y\)-axis, it lays exactly on top of the curve to the left of the \(y\)-axis. In this case, we say the function has symmetry about the \(y\)-axis. On the other hand, consider the function \(f(x)=x^3-4x\) shown in Figure 1.49(b). If we take the graph and rotate it \(180^{\circ}\) about the origin, the new graph will look exactly the same. In this case, we say the function has symmetry about the origin.
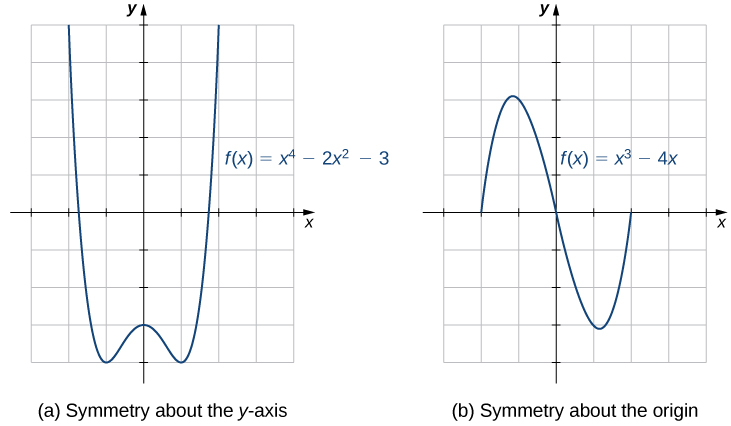
If we are given the graph of a function, it is easy to see whether the graph has one of these symmetry properties. But without a graph, how can we determine algebraically whether a function \(f\) has symmetry? Looking at Figure 1.49(a) again, we see that since \(f\) is symmetric about the \(y\)-axis, if the point \((x,y)\) is on the graph, the point \((-x,y)\) is on the graph. In other words, \(f(-x)=f(x).\) If a function \(f\) has this property, we say \(f\) is an even function, which has symmetry about the \(y\)-axis. For example, \(f(x)=x^2\) is even because
In contrast, looking at Figure 1.49(b) again, if a function \(f\) is symmetric about the origin, then whenever the point \((x,y)\) is on the graph, the point \((-x,-y)\) is also on the graph. In other words, \(f(-x)=-f(x).\) If \(f\) has this property, we say \(f\) is an odd function, which has symmetry about the origin. For example, \(f(x)=x^3\) is odd because
Definition 1.50.
If \(f(x)=f(-x)\) for all \(x\) in the domain of \(f,\) then \(f\) is an even function. An even function is symmetric about the \(y\)-axis.
If \(f(-x)=-f(x)\) for all \(x\) in the domain of \(f,\) then \(f\) is an odd function. An odd function is symmetric about the origin.
Example 1.51. Even and Odd Functions.
Determine whether each of the following functions is even, odd, or neither.
\(\displaystyle f(x)=-5x^4+7x^2-2\)
\(\displaystyle f(x)=2x^5-4x+5\)
\(\displaystyle f(x)=\frac{3x}{x^2+1}\)
To determine whether a function is even or odd, we evaluate \(f(-x)\) and compare it to \(f(x)\) and \(-f(x).\)
\(f(-x)=-5(-x)^4+7(-x)^2-2=-5x^4+7x^2-2=f(x).\) Therefore, \(f\) is even.
\(f(-x)=2(-x)^5-4(-x)+5=-2x^5+4x+5.\) Now, \(f(-x)\neq f(x).\) Furthermore, noting that \(-f(x)=-2x^5+4x-5,\) we see that \(f(-x)\neq-f(x).\) Therefore, \(f\) is neither even nor odd.
\(f(-x)=3(-x)/(-x)^2+1=-3x/(x^2+1)=-[3x/(x^2+1)]=-f(x).\) Therefore, \(f\) is odd.
Checkpoint 1.52.
Determine whether \(f(x)=4x^3-5x\) is even, odd, or neither.
One symmetric function that arises frequently is the absolute value function, written as \(|x|.\) The absolute value function is defined as
Some students describe this function by stating that it “makes everything positive.” By the definition of the absolute value function, we see that if \(x \lt 0,\) then \(|x|=-x \gt 0,\) and if \(x\gt 0,\) then \(|x|=x\gt 0.\) However, for \(x=0,|x|=0.\) Therefore, it is more accurate to say that for all nonzero inputs, the output is positive, but if \(x=0,\) the output \(|x|=0.\) We conclude that the range of the absolute value function is \(\{y|y \geq 0\}.\) In Figure 1.53, we see that the absolute value function is symmetric about the \(y\)-axis and is therefore an even function.
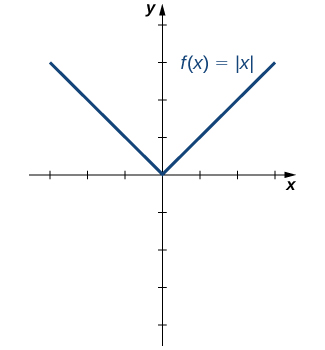
Example 1.54. Working with the Absolute Value Function.
Find the domain and range of the function \(f(x)=2|x-3|+4.\)
Since the absolute value function is defined for all real numbers, the domain of this function is \((-\infty,\infty).\) Since \(|x-3|\geq 0\) for all \(x,\) the function \(f(x)=2|x-3|+4\geq 4.\) Therefore, the range is, at most, the set \(\{y|y\geq 4\}.\) To see that the range is, in fact, this whole set, we need to show that for \(y\geq 4\) there exists a real number \(x\) such that
A real number \(x\) satisfies this equation as long as
Since \(y\geq 4,\) we know \(y-4\geq 0,\) and thus the right-hand side of the equation is nonnegative, so it is possible that there is a solution. Furthermore,
Therefore, we see there are two solutions:
The range of this function is \(\{y|y\geq 4\}.\)
Checkpoint 1.55.
For the function \(f(x)=|x+2|-4,\) find the domain and range.
Subsection 1.3.4 Key Concepts
A function is a mapping from a set of inputs to a set of outputs with exactly one output for each input.
If no domain is stated for a function \(y=f(x),\) the domain is considered to be the set of all real numbers \(x\) for which the function is defined.
When sketching the graph of a function \(f,\) each vertical line may intersect the graph, at most, once.
A function may have any number of zeros, but it has, at most, one \(y\)-intercept.
To define the composition \(g\circ f,\) the range of \(f\) must be contained in the domain of \(g.\)
Even functions are symmetric about the \(y\)-axis whereas odd functions are symmetric about the origin.
Subsection 1.3.5 Key Equations
Composition of two functions \((g\circ f)(x)=g(f(x))\)
Absolute value function
\begin{equation*} f(x)=\begin{cases}x \amp x \lt 0 \\ x \amp x \geq 0\end{cases}\text{.} \end{equation*}
This book is a custom edition based on OpenStax Calculus Volume 1. You can download the original for free at https://openstax.org/details/books/calculus-volume-1. 1
Additional practice exercises are available in at the bottom on this section in OpenStax Calculus Volume 1: https://openstax.org/books/calculus-volume-1/pages/1-1-review-of-functions
https://openstax.org/details/books/calculus-volume-1