The Limit Laws

Skip to main content

\(\newcommand{\N}{\mathbb N} \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\R}{\mathbb R} \newcommand{\lt}{<} \newcommand{\gt}{>} \newcommand{\amp}{&} \definecolor{fillinmathshade}{gray}{0.9} \newcommand{\fillinmath}[1]{\mathchoice{\colorbox{fillinmathshade}{$\displaystyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\textstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptstyle \phantom{\,#1\,}$}}{\colorbox{fillinmathshade}{$\scriptscriptstyle\phantom{\,#1\,}$}}} \)

Section 2.3 The Limit Laws

Learning Objectives.

Recognize the basic limit laws.
Use the limit laws to evaluate the limit of a function.
Evaluate the limit of a function by factoring.
Use the limit laws to evaluate the limit of a polynomial or rational function.
Evaluate the limit of a function by factoring or by using conjugates.

In the previous section, we evaluated limits by looking at graphs or by constructing a table of values. In this section, we establish laws for calculating limits and learn how to apply these laws. We begin by restating two useful limit results from the previous section. These two results, together with the limit laws, serve as a foundation for calculating many limits.

Subsection 2.3.1 Evaluating Limits with the Limit Laws

The first two limit laws were stated in Theorem 2.34 and we repeat them here. These basic results, together with the other limit laws, allow us to evaluate limits of many algebraic functions.

Theorem 2.62. Basic Limit Results.

For any real number \(a\) and any constant \(c\text{,}\)

\(\displaystyle \lim_{x \to a }x=a\)
\(\displaystyle \lim_{x \to a }c=c\)

Example 2.63. Evaluating a Basic Limit.

Evaluate each of the following limits using Theorem 2.62.

\(\displaystyle \lim_{x \to 2 }x\)
\(\displaystyle \lim_{x \to 2 }5\)

The limit of \(x\) as \(x\) approaches \(a\) is \(a\text{:}\) \(\displaystyle{\lim_{x \to 2 }x=2.}\)
The limit of a constant is that constant: \(\displaystyle{\lim_{x \to 2 }5=5.}\)

We now take a look at the limit laws, the individual properties of limits. The proofs that these laws hold are omitted here.

Theorem 2.64. Limit Laws.

Let \(f(x)\) and \(g(x)\) be defined for all \(x\neq a\) over some open interval containing \(a\text{.}\) Assume that \(L \) and \(M \) are real numbers such that \(\displaystyle{\lim_{x \to a }f(x)=L}\) and \(\displaystyle{\lim_{x \to a }g(x)=M.}\) Let \(c\) be a constant. Then, each of the following statements holds:

Sum law for limits: \(\displaystyle{\lim_{x \to a }(f(x)+g(x))=\lim_{x \to a }f(x)+\lim_{x \to a }g(x)=L+M}\)

Difference law for limits: \(\displaystyle{\lim_{x \to a }(f(x)-g(x))=\lim_{x \to a }f(x)-\lim_{x \to a }g(x)=L-M}\)

Constant multiple law for limits: \(\displaystyle{\lim_{x \to a }cf(x)=c\cdot \lim_{x \to a }f(x)=cL}\)

Product law for limits: \(\displaystyle{\lim_{x \to a }(f(x)\cdot g(x))=\lim_{x \to a }f(x)\cdot \lim_{x \to a }g(x)=L\cdot M}\)

Quotient law for limits: \(\displaystyle{\lim_{x \to a }\frac{f(x)}{g(x)}=\displaystyle{\frac{\lim_{x \to a }f(x)}{\lim_{x \to a }g(x)}}=\frac{L}{M}}\) for \(M\neq 0\)

Power law for limits: \(\displaystyle{\lim_{x \to a }(f(x))^n=\left(\lim_{x \to a }f(x)\right)^n=L^n}\) for every positive integer \(n\text{.}\)

Root law for limits: \(\displaystyle{\lim_{x \to a }\sqrt[n]{f(x)}=\sqrt[n]{\lim_{x \to a }f(x)}=\sqrt[n]{L}}\) for all \(L\) if \(n\) is odd and for \(L\geq 0\) if \(n\) is even.

We now practice applying these limit laws to evaluate a limit.

Example 2.65. Evaluating a Limit Using Limit Laws.

Use the limit laws to evaluate \(\displaystyle{\lim_{x \to -3 }(4x+2).}\)

Let’s apply the limit laws one step at a time to be sure we understand how they work. We need to keep in mind the requirement that, at each application of a limit law, the new limits must exist for the limit law to be applied.

\begin{align*} \lim_{x \to -3 }(4x+2) \amp=\lim_{x \to -3 }4x+\lim_{x \to -3 }2 \amp\text{ Apply the sum law. }\\ \amp=4\cdot \lim_{x \to -3 }x+\lim_{x \to -3 }2\amp\text{ Apply the constant multiple law. }\\ \amp=4\cdot (-3)+2=-10. \amp\text{ Apply the basic limit results and simplify. } \end{align*}

Example 2.66. Using Limit Laws Repeatedly.

Use the limit laws to evaluate \(\displaystyle{\lim_{x \to 2 }\frac{2x^2-3x+1}{x^3+4}.}\)

To find this limit, we need to apply the limit laws several times. Again, we need to keep in mind that as we rewrite the limit in terms of other limits, each new limit must exist for the limit law to be applied.

\begin{align*} \lim_{x \to 2 }\frac{2x^2-3x+1}{x^3+4}\amp=\displaystyle{\frac{\lim_{x \to 2 }(2x^2-3x+1)}{\lim_{x \to 2 }(x^3+4)}}\amp\text{ Apply the quotient law, making sure that. } (2)^3+4\neq 0\\ \amp=\displaystyle{\frac{2\cdot \lim_{x \to 2 }x^2-3\cdot \lim_{x \to 2 }x+\lim_{x \to 2 }1}{\lim_{x \to 2 }x^3+\lim_{x \to 2 }4}}\amp\text{ Apply the sum law and constant multiple law. }\\ \amp=\displaystyle{\frac{2\cdot \lim_{x \to 2 }x^2-3\cdot \lim_{x \to 2 }x+\lim_{x \to 2 }1}{(\lim_{x \to 2 }x)^3+\lim_{x \to 2 }4}}\amp\text{ Apply the power law. }\\ \amp=\displaystyle{\frac{2(4)-3(2)+1}{(2)^3+4}=\frac{1}{4}.}\amp\text{ Apply the basic limit laws and simplify. } \end{align*}

Checkpoint 2.67.

Use the limit laws to evaluate \(\displaystyle{\lim_{x \to 6 }(2x-1)\sqrt{x+4}.}\) In each step, indicate the limit law applied.

Begin by applying the product law.

\(11\sqrt{10}\)

Subsection 2.3.2 Limits of Polynomial and Rational Functions

By now you have probably noticed that, in each of the previous examples, it has been the case that \(\lim_{x \to a }f(x)=f(a).\) This is not always true, but it does hold for all polynomials for any choice of \(a\) and for all rational functions at all values of \(a\) for which the rational function is defined.

Theorem 2.68. Limits of Polynomial and Rational Functions.

Let \(p(x)\) and \(q(x)\) be polynomial functions. Let \(a\) be a real number. Then,

\begin{equation*} \lim_{x \to a }p(x)=p(a) \end{equation*}

\begin{equation*} \lim_{x \to a }\frac{p(x)}{q(x)}=\frac{p(a)}{q(a)} \text{ when } q(a)\neq 0. \end{equation*}

Example 2.69 applies this result.

Example 2.69. Evaluating a Limit of a Rational Function.

Evaluate the \(\displaystyle{\lim_{x \to 3 }\frac{2x^2-3x+1}{5x+4}.}\)

Since 3 is in the domain of the rational function \(f(x)=\frac{2x^2-3x+1}{5x+4},\) we can calculate the limit by substituting 3 for \(x\) into the function. Thus,

\begin{equation*} \lim_{x \to 3 }\frac{2x^2-3x+1}{5x+4}=\frac{10}{19}. \end{equation*}

Checkpoint 2.70.

Evaluate \(\displaystyle{\lim_{x \to -2 }(3x^3-2x+7).}\)

Use Theorem 2.68

-13;

Subsection 2.3.3 Additional Limit Evaluation Techniques

As we have seen, we may evaluate easily the limits of polynomials and limits of some (but not all) rational functions by direct substitution. However, as we saw in the introductory section on limits, it is certainly possible for \(\displaystyle{\lim_{x \to a }f(x)}\) to exist when \(f(a)\) is undefined. The following observation allows us to evaluate many limits of this type:

If for all \(x\neq a,f(x)=g(x)\) over some open interval containing \(a\text{,}\) then \(\displaystyle{\lim_{x \to a }f(x)=\lim_{x \to a }g(x).}\)

To understand this idea better, consider the limit \(\displaystyle{\lim_{x \to 1 }\frac{x^2-1}{x-1}.}\)

The function

\begin{align*} f(x)\amp=\frac{x^2-1}{x-1}\\ \amp=\frac{(x-1)(x+1)}{x-1} \end{align*}

and the function \(g(x)=x+1\) are identical for all values of \(x\neq 1.\) The graphs of these two functions are shown in Figure 2.71.

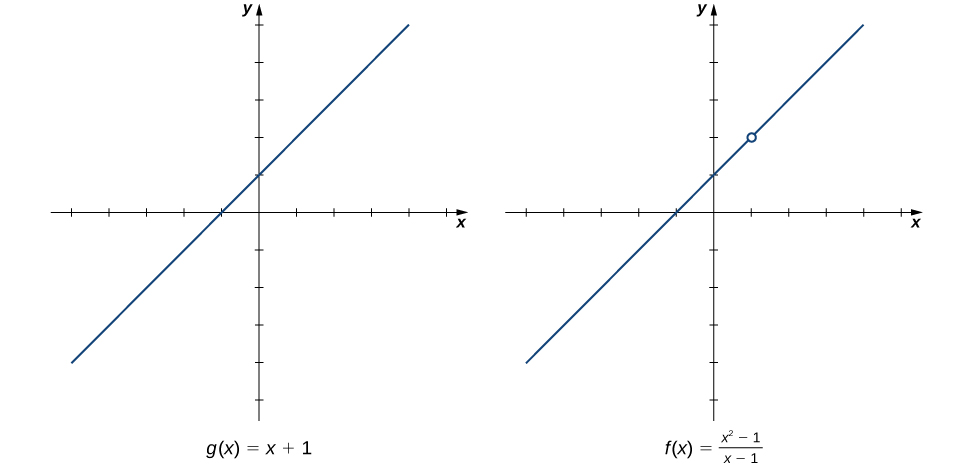
"Two graphs side by side. The first is a graph of g(x) = x + 1, a linear function with y intercept at (0,1) and x intercept at (-1,0). The second is a graph of f(x) = (x^2 – 1) / (x – 1). This graph is identical to the first for all x not equal to 1, as there is an open circle at (1,2) in the second graph." — Figure 2.71. The graphs of \(f(x)\) and \(g(x)\) are identical for all \(x\neq 1.\) Their limits at 1 are equal.

We see that

\begin{align*} \lim_{x \to 1 }\frac{x^2-1}{x-1}\amp=\lim_{x \to 1 }\frac{(x-1)(x+1)}{(x-1)}\\ \amp=\lim_{x \to 1 }(x+1)\\ \amp=2. \end{align*}

The limit has the form \(\displaystyle{\lim_{x \to a }\frac{f(x)}{g(x)},}\) where \(\displaystyle{\lim_{x \to a }f(x)=0}\) and \(\displaystyle{\lim_{x \to a }g(x)=0.}\) (In this case, we say that \(f(x)/g(x)\) has the indeterminate form \(0/0\text{ .) }\) The following Problem-Solving Strategy provides a general outline for evaluating limits of this type.

Note 2.72. Problem-Solving Strategy: Calculating a Limit When \(f(x)/g(x)\) has the Indeterminate Form 0/0.

First, we need to make sure that our function has the appropriate form and cannot be evaluated immediately using the limit laws.
We then need to find a function that is equal to \(h(x)=f(x)/g(x)\) for all \(x\neq a\) over some interval containing \(a\text{.}\) To do this, we may need to try one or more of the following steps:
1. If \(f(x)\) and \(g(x)\) are polynomials, we should factor each function and cancel out any common factors.
2. If the numerator or denominator contains a difference involving a square root, we should try multiplying the numerator and denominator by the conjugate of the expression involving the square root.
3. If \(f(x)/g(x)\) is a complex fraction, we begin by simplifying it.
Last, we apply the limit laws.

The next examples demonstrate the use of this Problem-Solving Strategy. Example 2.73 illustrates the factor-and-cancel technique; Example 2.75 shows multiplying by a conjugate. In Example 2.77, we look at simplifying a complex fraction.

Example 2.73. Evaluating a Limit by Factoring and Canceling.

Evaluate \(\displaystyle{\lim_{x \to 3 }\frac{x^2-3x}{2x^2-5x-3}.}\)

Step 1. The function \(f(x)=\frac{x^2-3x}{2x^2-5x-3}\) is undefined for \(x=3.\) In fact, if we substitute 3 into the function we get \(0/0,\) which is undefined. Factoring and canceling is a good strategy:

\begin{equation*} \lim_{x \to 3 }\frac{x^2-3x}{2x^2-5x-3}=\lim_{x \to 3 }\frac{x(x-3)}{(x-3)}{(2x+1)} \end{equation*}

Step 2. For all \(x\neq 3,\frac{x^2-3x}{2x^2-5x-3}=\frac{x}{2x+1}.\) Therefore,

\begin{equation*} \lim_{x \to 3 }\frac{x(x-3)}{(x-3)}{(2x+1)}=\lim_{x \to 3 }\frac{x}{2x+1}. \end{equation*}

Step 3. Evaluate using the limit laws:

\begin{equation*} \lim_{x \to 3 }\frac{x}{2x+1}=\frac{3}{7}. \end{equation*}

Checkpoint 2.74.

Evaluate \(\displaystyle{\lim_{x \to -3 }\frac{x^2+4x+3}{x^2-9}.}\)

Follow the steps in the Problem-Solving Strategy and Example 2.73.

\(\frac{1}{3}\)

Example 2.75. Evaluating a Limit by Multiplying by a Conjugate.

Evaluate \(\displaystyle{\lim_{x \to -1 }\frac{\sqrt{x+2}-1}{x+1}.}\)

Step 1. \(\frac{\sqrt{x+2}-1}{x+1}\) has the form \(0/0\) at -1. Let’s begin by multiplying by \(\sqrt{x+2}+1,\) the conjugate of \(\sqrt{x+2}-1,\) on the numerator and denominator:

\begin{equation*} \lim_{x \to -1 }\frac{\sqrt{x+2}-1}{x+1}=\lim_{x \to -1 }\frac{\sqrt{x+2}-1}{x+1}\cdot \frac{\sqrt{x+2}+1}{\sqrt{x+2}+1}. \end{equation*}

Step 2. We then multiply out the numerator. We don’t multiply out the denominator because we are hoping that the \((x+1)\) in the denominator cancels out in the end:

\begin{equation*} =\lim_{x \to -1 }\frac{x+1}{(x+1)}{(\sqrt{x+2}+1)}. \end{equation*}

Step 3. Then we cancel:

\begin{equation*} =\lim_{x \to -1 }\frac{1}{\sqrt{x+2}+1}. \end{equation*}

Step 4. Last, we apply the limit laws:

\begin{equation*} \lim_{x \to -1 }\frac{1}{\sqrt{x+2}+1}=\frac{1}{2}. \end{equation*}

Checkpoint 2.76.

Evaluate \(\displaystyle{\lim_{x \to 5 }\frac{\sqrt{x-1}-2}{x-5}.}\)

Follow the steps in the Problem-Solving Strategy and Example 2.75.

\(\frac{1}{4}\)

Example 2.77. Evaluating a Limit by Simplifying a Complex Fraction.

Evaluate \(\displaystyle{\lim_{x \to 1 }\frac{\frac{1}{x+1}-\frac{1}{2}}{x-1}.}\)

Step 1. \(\frac{\frac{1}{x+1}-\frac{1}{2}}{x-1}\) has the form \(0/0\) at 1. We simplify the algebraic fraction by multiplying by \(2(x+1)/2(x+1):\)

\begin{equation*} \lim_{x \to 1 }\frac{\frac{1}{x+1}-\frac{1}{2}}{x-1}=\lim_{x \to 1 }\frac{\frac{1}{x+1}-\frac{1}{2}}{x-1}\cdot \frac{2(x+1)}{2(x+1)}. \end{equation*}

Step 2. Next, we multiply through the numerators. Do not multiply the denominators because we want to be able to cancel the factor \((x-1)\text{ : }\)

\begin{equation*} =\lim_{x \to 1 }\frac{2-(x+1)}{2(x-1)}{(x+1)}. \end{equation*}

Step 3. Then, we simplify the numerator:

\begin{equation*} =\lim_{x \to 1 }\frac{-x+1}{2(x-1)(x+1)}. \end{equation*}

Step 4. Now we factor out -1 from the numerator:

\begin{equation*} =\lim_{x \to 1 }\frac{-(x-1)}{2(x-1)(x+1)}. \end{equation*}

Step 5. Then, we cancel the common factors of \((x-1)\text{ : }\)

\begin{equation*} =\lim_{x \to 1 }\frac{-1}{2(x+1)}. \end{equation*}

Step 6. Last, we evaluate using the limit laws:

\begin{equation*} \lim_{x \to 1 }\frac{-1}{2(x+1)}=-\frac{1}{4}. \end{equation*}

Checkpoint 2.78.

Evaluate \(\displaystyle{\lim_{x \to -3 }\frac{\frac{1}{x+2}+1}{x+3}.}\)

Follow the steps in the Problem-Solving Strategy and Example 2.77.

-1

Example 2.79 does not fall neatly into any of the patterns established in the previous examples. However, with a little creativity, we can still use these same techniques.

Example 2.79. Evaluating a Limit When the Limit Laws Do Not Apply.

Evaluate \(\displaystyle{\lim_{x \to 0 }\left(\frac{1}{x}+\frac{5}{x(x-5)}\right).}\)

Both \(1/x\) and \(5/x(x-5)\) fail to have a limit at zero. Since neither of the two functions has a limit at zero, we cannot apply the sum law for limits; we must use a different strategy. In this case, we find the limit by performing addition and then applying one of our previous strategies. Observe that

\begin{align*} \frac{1}{x}+\frac{5}{x(x-5)}\amp=\frac{x-5+5}{x(x-5)}\\ \amp=\frac{x}{x(x-5)}. \end{align*}

Thus,

\begin{align*} \lim_{x \to 0 }\left(\frac{1}{x}+\frac{5}{x(x-5)}\right)\amp=\lim_{x \to 0 }\frac{x}{x(x-5)}\\ \amp=\lim_{x \to 0 }\frac{1}{x-5}\\ \amp=-\frac{1}{5}. \end{align*}

Checkpoint 2.80.

Evaluate \(\displaystyle{\lim_{x \to 3 }\left(\frac{1}{x-3}-\frac{4}{x^2-2x-3}\right).}\)

Use the same technique as Example 2.79. Don’t forget to factor \(x^2-2x-3\) before getting a common denominator.

\(\frac{1}{4}\)

Let’s now revisit one-sided limits. Simple modifications in the limit laws allow us to apply them to one-sided limits. For example, to apply the limit laws to a limit of the form \(\displaystyle{\lim_{x\to a^-} h(x),}\) we require the function \(h(x)\) to be defined over an open interval of the form \((b,a);\) for a limit of the form \(\displaystyle{\lim_{x \to a^+} h(x),}\) we require the function \(h(x)\) to be defined over an open interval of the form \((a,c).\) Example 2.81 illustrates this point.

Example 2.81. Evaluating a One-Sided Limit Using the Limit Laws.

Evaluate each of the following limits, if possible.

\(\displaystyle \lim_{x \to 3^-}\sqrt{x-3}\)
\(\displaystyle \lim_{x \to 3^+}\sqrt{x-3}\)

Figure 2.82 illustrates the function \(f(x)=\sqrt{x-3}\) and aids in our understanding of these limits.

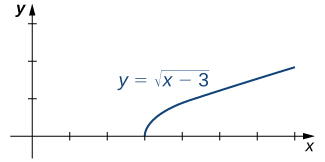
"A graph of the function f(x) = sqrt(x-3). Visually, the function looks like the top half of a parabola opening to the right with vertex at (3,0)." — Figure 2.82. The graph shows the function \(f(x)=\sqrt{x-3}.\)

The function \(f(x)=\sqrt{x-3}\) is defined over the interval \([3,+\infty).\) Since this function is not defined to the left of 3, we cannot apply the limit laws to compute \(\displaystyle{\lim_{x \to 3^-}\sqrt{x-3}.}\) In fact, since \(f(x)=\sqrt{x-3}\) is undefined to the left of 3, \(\displaystyle{\lim_{x \to 3^-}\sqrt{x-3}}\) does not exist.
Since \(f(x)=\sqrt{x-3}\) is defined to the right of 3, the limit laws do apply to \(\displaystyle{\lim_{x \to 3^+}\sqrt{x-3}.}\) By applying these limit laws we obtain \(\displaystyle{\lim_{x \to 3^+}\sqrt{x-3}=0.}\)

In Example 2.83 we look at one-sided limits of a piecewise-defined function and use these limits to draw a conclusion about a two-sided limit of the same function.

Example 2.83.

For \(f(x)=\begin{cases} 4x-3\amp\text{ if } x\lt 2\\ (x-3)^2\amp\text{ if } x\geq 2 \end{cases},\) evaluate each of the following limits:

\(\displaystyle \lim_{x \to 2^-}f(x)\)
\(\displaystyle \lim_{x \to 2^+}f(x)\)
\(\displaystyle \lim_{x \to 2 }f(x)\)

Figure 2.84 illustrates the function \(f(x)\) and aids in our understanding of these limits.

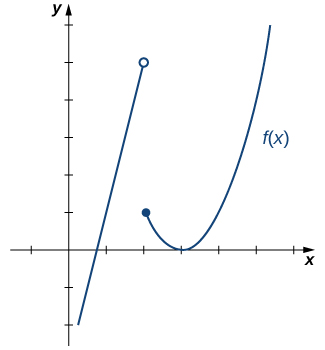
"The graph of a piecewise function with two segments. For x\lt 2, the function is linear with the equation 4x-3. There is an open circle at (2,5). The second segment is a parabola and exists for x\gt =2, with the equation (x-3)^2. There is a closed circle at (2,1). The vertex of the parabola is at (3,0)." — Figure 2.84. This graph shows a function \(f(x).\)

Since \(f(x)=4x-3\) for all \(x\) in \((-\infty,2),\) replace \(f(x)\) in the limit with \(4x-3\) and apply the limit laws:
\begin{equation*} \lim_{x \to 2^-}f(x)=\lim_{x \to 2^-}(4x-3)=5. \end{equation*}
Since \(f(x)=(x-3)^2\) for all \(x\) in \((2,+\infty),\) replace \(f(x)\) in the limit with \((x-3)^2\) and apply the limit laws:
\begin{equation*} \lim_{x \to 2^+}f(x)=\lim_{x \to 2^+}(x-3)^2=1. \end{equation*}
Since \(\displaystyle{\lim_{x \to 2^-}f(x)=5}\) and \(\displaystyle{\lim_{x \to 2^+}f(x)=1,}\) we conclude that \(\displaystyle{\lim_{x \to 2 }f(x)}\) does not exist.

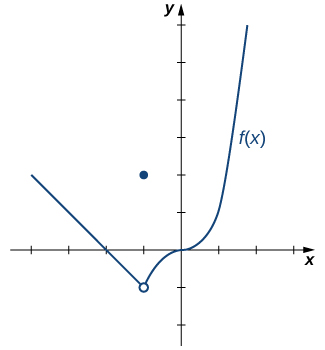
Checkpoint 2.85.

Graph \(f(x)=\begin{cases}-x-2 \amp \text{ if } x\lt -1 \\ 2 \amp \text{ if } x=-1 \\ x^3 \amp \text{ if } x\gt -1 \end{cases} \) and evaluate \(\displaystyle{\lim_{x\to -1^-}f(x).}\)

Use the method in Example 2.83 to evaluate the limit.

$"The graph of a piecewise function with three segments. The first is a linear function, -x-2, for x\lt -1. The x intercept is at (-2,0), and there is an open circle at (-1,-1). The next segment is simply the point (-1, 2). The third segment is the function x^3 for x \gt -1, which crossed the x axis and y axis at the origin."$

\(\displaystyle{\lim_{x\to -1^-}f(x)=-1}\)

We now turn our attention to evaluating a limit of the form \(\displaystyle{\lim_{x \to a }\frac{f(x)}{g(x)},}\) where \(\displaystyle{\lim_{x \to a }f(x)=K,}\) where \(K\neq 0\) and \(\displaystyle{\lim_{x \to a }g(x)=0.}\) That is, \(f(x)/g(x)\) has the form \(K/0,K\neq 0\) at \(a\text{.}\)

Example 2.86. Evaluating a Limit of the Form \(K/0,K\neq 0\) Using the Limit Laws.

Evaluate \(\displaystyle{\lim_{x \to 2^-}\frac{x-3}{x^2-2x}.}\)

Step 1. After substituting in \(x=2,\) we see that this limit has the form \(-1/0.\) That is, as \(x\) approaches 2 from the left, the numerator approaches -1; and the denominator approaches 0. Consequently, the magnitude of \(\frac{x-3}{x(x-2)}\) becomes infinite. To get a better idea of what the limit is, we need to factor the denominator:

\begin{equation*} \lim_{x \to 2^-}\frac{x-3}{x^2-2x}=\lim_{x \to 2^-}\frac{x-3}{x(x-2)}. \end{equation*}

Step 2. Since \(x-2\) is the only part of the denominator that is zero when 2 is substituted, we then separate \(1/(x-2)\) from the rest of the function:

\begin{equation*} =\lim_{x \to 2^-}\frac{x-3}{x}\cdot \frac{1}{x-2}. \end{equation*}

Step 3. \(\displaystyle{\lim_{x \to 2^-}\frac{x-3}{x}=-\frac{1}{2}}\) and \(\displaystyle{\lim_{x \to 2^-}\frac{1}{x-2}=-\infty.}\) Therefore, the product of \((x-3)/x\) and \(1/(x-2)\) has a limit of \(+\infty\)

\begin{equation*} \lim_{x \to 2^-}\frac{x-3}{x^2-2x}=+\infty. \end{equation*}

Checkpoint 2.87.

Evaluate \(\displaystyle{\lim_{x \to 1 }\frac{x+2}{(x-1)^2}.}\)

Use the methods from Example 2.86.

\(+\infty\)

Subsection 2.3.4 Key Concepts

The limit laws allow us to evaluate limits of functions without having to go through step-by-step processes each time.
For polynomials and rational functions, \(\displaystyle{\lim_{x \to a }f(x)=f(a).}\)
You can evaluate the limit of a function by factoring and canceling, by multiplying by a conjugate, or by simplifying a complex fraction.

Subsection 2.3.5 Key Equations

Basic Limit Results \(\displaystyle{\lim_{x \to a }x=a.\; \lim_{x \to a }c=c}\)

This book is a custom edition based on OpenStax Calculus Volume 1. You can download the original for free at https://openstax.org/details/books/calculus-volume-1.