Skip to main content

Section 1.8 Logarithmic Functions

Learning Objectives.

  1. Identify the form of a logarithmic function.

  2. Explain the relationship between exponential and logarithmic functions.

  3. Describe how to calculate a logarithm to a different base.

In this section we examine logarithmic functions. We use the properties of these functions to solve equations involving exponential and logarithmic terms. Note: This the second half of section 1.5 in the original version of OpenStax Calculus.

Subsection 1.8.1 Logarithmic Functions

Using our understanding of exponential functions, we can discuss their inverses, which are the logarithmic functions. These come in handy when we need to consider any phenomenon that varies over a wide range of values, such as pH in chemistry or decibels in sound levels.

The exponential function \(f(x)=b^x\) is one-to-one, with domain \((-\infty,\infty)\) and range \((0,\infty).\) Therefore, it has an inverse function, called the logarithmic function with base \(b.\) For any \(b\gt 0,b\neq 1,\) the logarithmic function with base b, denoted \(\log_b ,\) has domain \((0,\infty)\) and range \((-\infty,\infty),\) and satisfies

\begin{equation*} \log_b (x)=y \text{ if and only if } b^y=x. \end{equation*}

For example,

\begin{align*} \log_2 (8)=3 \amp \text{ since } 2^3=8,\\ \log_{10}\left( \frac{1}{100}\right)=−2 \amp \text{ since } 10^{−2}= \frac{1}{10^2}= \frac{1}{100},\\ \log_b (1)=0 \amp \text{ since } b^0=1 \text{ for any base } b\gt 0. \end{align*}

Furthermore, since \(y=\log_b (x)\) and \(y=b^x\) are inverse functions,

\begin{equation*} \log_b (b^x)=x \text{ and } b^{\log_b (x)}=x. \end{equation*}

The most commonly used logarithmic function is the function \(\log_e .\) Since this function uses natural \(e\) as its base, it is called the natural logarithm. Here we use the notation \(\ln(x)\) or \(\ln x\) to mean \(\log_e (x).\) For example,

\begin{equation*} \ln(e)=\log_e (e)=1,\ln(e^3)=\log_e (e^3)=3,\ln(1)=\log_e (1)=0. \end{equation*}

Since the functions \(f(x)=e^x\) and \(g(x)=\ln(x)\) are inverses of each other,

\begin{equation*} \ln(e^x)=x \text{ and } e^{\ln x}=x, \end{equation*}

and their graphs are symmetric about the line \(y=x\) (Figure 1.122).

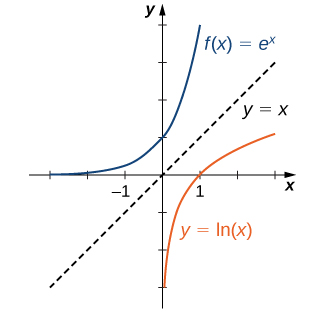
"An image of a graph. The x axis runs from -3 to 3 and the y axis runs from -3 to 4. The graph is of two functions. The first function is “f(x) = e to power of x”, an increasing curved function that starts slightly above the x axis. The y intercept is at the point (0, 1) and there is no x intercept. The second function is “f(x) = ln(x)”, an increasing curved function. The x intercept is at the point (1, 0) and there is no y intercept. A dotted line with label “y = x” is also plotted on the graph, to show that the functions are mirror images over this line."
Figure 1.122. The functions \(y=e^x\) and \(y=\ln(x)\) are inverses of each other, so their graphs are symmetric about the line \(y=x.\)

Another frequently used logarithmic function is the function \(\log_{10} .\) It is called the common logarithm. Here we use the notation \(\log(x)\) or \(\log x\) to mean \(\log_{10} (x).\) For example,

\begin{equation*} \log(10)=\log_{10} (10)=1,\log(1000)=\log_{10}(10^3)=3,\log(1)=\log_{10} (1)=0. \end{equation*}

Note 1.123. Media.

At this site 1  you can see an example of a base-10 logarithmic scale.

In general, for any base \(b\gt 0,b\neq 1,\) the function \(g(x)=\log_b (x)\) is symmetric about the line \(y=x\) with the function \(f(x)=b^x.\) Using this fact and the graphs of the exponential functions, we graph functions \(\log_b \) for several values of \(b\gt 1\) (Figure 1.124).

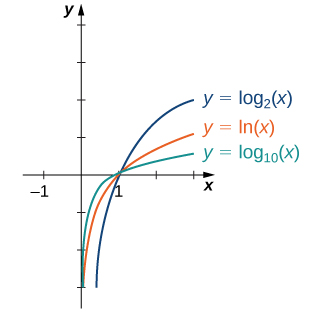
"An image of a graph. The x axis runs from -3 to 3 and the y axis runs from 0 to 4. The graph is of three functions. All three functions a log functions that are increasing curved functions that start slightly to the right of the y axis and have an x intercept at (1, 0). The first function is “y = log base 10 (x)”, the second function is “f(x) = ln(x)”, and the third function is “y = log base 2 (x)”. The third function increases the most rapidly, the second function increases next most rapidly, and the third function increases the slowest."
Figure 1.124. Graphs of \(y=\log_b (x)\) are depicted for \(b=2,e,10.\)

Before solving some equations involving exponential and logarithmic functions, let’s review the basic properties of logarithms.

Note 1.125. Rule: Properties of Logarithms.

If \(a,b,c\gt 0,b\neq 1,\) and \(r\) is any real number, then

\begin{align*} 1. \log_b (ac)=\log_b (a)+\log_b (c) \amp \text{ (Product property) }\\ 2. \log_b \left( \frac{a}{c}\right)=\log_b (a)−\log_b (c) \amp \text{ (Quotient property) }\\ 3. \log_b (a^r)=r\log_b (a) \amp \text{ (Power property) } \end{align*}

Example 1.126. Solving Equations Involving Exponential Functions.

Solve each of the following equations for \(x.\)

  1. \(\displaystyle 5^x=2\)

  2. \(\displaystyle e^x+6e^{-x}=5\)

Solution.

  1. Applying the natural logarithm function to both sides of the equation, we have

    \begin{equation*} \ln5^x=\ln 2. \end{equation*}
    Using the power property of logarithms,
    \begin{equation*} x\ln 5=\ln 2. \end{equation*}
    Therefore, \(x=\ln 2/\ln 5.\)

  2. Multiplying both sides of the equation by \(e^x,\) we arrive at the equation

    \begin{equation*} e^{2x}+6=5e^x. \end{equation*}
    Rewriting this equation as
    \begin{equation*} e^{2x}−5e^x+6=0, \end{equation*}
    we can then rewrite it as a quadratic equation in \(e^x.\)
    \begin{equation*} (e^x)^2−5(e^x)+6=0. \end{equation*}
    Now we can solve the quadratic equation. Factoring this equation, we obtain
    \begin{equation*} (e^x−3)(e^x−2)=0. \end{equation*}
    Therefore, the solutions satisfy \(e^x=3\) and \(e^x=2.\) Taking the natural logarithm of both sides gives us the solutions \(x=\ln 3,\ln 2.\)

Checkpoint 1.127.

Solve \(e^{-x}/(3+e^{-x})=1/2.\)

Hint.

First solve the equation for \(e^{-x}.\)

Solution.

\(x=\frac{\ln 3}{2}\)

Example 1.128. Solving Equations Involving Logarithmic Functions.

Solve each of the following equations for \(x.\)

  1. \(\displaystyle \ln\left(\frac{1}{x}\right)=4\)

  2. \(\displaystyle \log_{10}\sqrt{x}+\log_{10}x=2\)

  3. \(\displaystyle \ln(2x)−3\ln(x^2)=0\)

Solution.

  1. By the definition of the natural logarithm function,

    \begin{equation*} \ln\left(\frac{1}{x}\right)=4 \text{ if and only if } e^4=\frac{1}{2}. \end{equation*}
    Therefore, the solution is \(x=1/e^4.\)

  2. Using the product and power properties of logarithmic functions, rewrite the left-hand side of the equation as

    \begin{equation*} \log_{10}\sqrt{x}+\log_{10}x=\log_{10}x\sqrt{x}=\log_{10}x^{3/2}=\frac{3}{2}\log_{10}x. \end{equation*}
    Therefore, the equation can be rewritten as
    \begin{equation*} \frac{3}{2}\log_{10}x=2 \text{ or } \log_{10}x=\frac{4}{3}. \end{equation*}
    The solution is \(x=10^{4/3}=10\sqrt[3]{10}.\)

  3. Using the power property of logarithmic functions, we can rewrite the equation as \(\ln(2x)−\ln(x^6)=0.\) Using the quotient property, this becomes

    \begin{equation*} \ln\left(\frac{2}{x^5}\right)=0. \end{equation*}
    Therefore, \(2/x^5=1,\) which implies \(x=\sqrt[5]{2}.\) We should then check for any extraneous solutions.

Checkpoint 1.129.

Solve \(\ln(x^3)−4>\ln(x)=1.\)

Hint.

First use the power property, then use the product property of logarithms.

Solution.

\(x=\frac{1}{e}\)

When evaluating a logarithmic function with a calculator, you may have noticed that the only options are \(\log_{10}\) or log, called the common logarithm, or ln, which is the natural logarithm. However, exponential functions and logarithm functions can be expressed in terms of any desired base \(b.\) If you need to use a calculator to evaluate an expression with a different base, you can apply the change-of-base formulas first. Using this change of base, we typically write a given exponential or logarithmic function in terms of the natural exponential and natural logarithmic functions.

Note 1.130. Rule: Change-of-Base Formulas.

Let \(a\gt 0,b\gt 0,\) and \(a\neq 1,b\neq 1.\)

  1. \(a^x=b^{\log_b a^x}\) for any real number \(x.\) If \(b=e,\) this equation reduces to \(a^x=e^{\log_e a^x}=e^{x\ln a}.\)

  2. \(\log_a x=\frac{\log_b x}{\log_b a}\) for any real number \(x\gt 0.\) If \(b=e,\) this equation reduces to \(\log_a x=\frac{\ln x}{\ln a}.\)

Example 1.131. Changing Bases.

Use a calculating utility to evaluate \(\log_{3}7\) with the change-of-base formula presented earlier.

Solution.

Use the second equation with \(a=3\) and \(e=3.\)

\(\log_{3}7=\frac{\ln 7}{\ln 3}≈1.77124.\)

Checkpoint 1.132.

Use the change-of-base formula and a calculating utility to evaluate \(\log_{4}6.\)

Hint.

Use the change of base to rewrite this expression in terms of expressions involving the natural logarithm function.

Solution.

\(1.29248\)

Example 1.133. Chapter Opener: The Richter Scale for Earthquakes.

"A photograph of an earthquake fault."
Figure 1.134. (credit: modification of work by Robb Hannawacker, NPS)

In 1935, Charles Richter developed a scale (now known as the Richter scale) to measure the magnitude of an earthquake. The scale is a base-10 logarithmic scale, and it can be described as follows: Consider one earthquake with magnitude \(R_1\) on the Richter scale and a second earthquake with magnitude \(R_2\) on the Richter scale. Suppose \(R_1\gt R_2,\) which means the earthquake of magnitude \(R_1\) is stronger, but how much stronger is it than the other earthquake? A way of measuring the intensity of an earthquake is by using a seismograph to measure the amplitude of the earthquake waves. If \(A_1\) is the amplitude measured for the first earthquake and \(A_2\) is the amplitude measured for the second earthquake, then the amplitudes and magnitudes of the two earthquakes satisfy the following equation:

\begin{equation*} R_1−R_2=\log_{10}\left(\frac{A_1}{A_2}\right). \end{equation*}

Consider an earthquake that measures 8 on the Richter scale and an earthquake that measures 7 on the Richter scale. Then,

\begin{equation*} 8−7=\log_{10}\left(\frac{A_1}{A_2}\right). \end{equation*}

Therefore,

\begin{equation*} \log_{10}\left(\frac{A_1}{A_2}\right)=1, \end{equation*}

which implies \(A_1/A_2=10\) or \(A_1=10A_2.\) Since \(A_1\) is 10 times the size of \(A_2,\) we say that the first earthquake is 10 times as intense as the second earthquake. On the other hand, if one earthquake measures 8 on the Richter scale and another measures 6, then the relative intensity of the two earthquakes satisfies the equation

\begin{equation*} \log_{10}\left(\frac{A_1}{A_2}\right)=8−6=2. \end{equation*}

Therefore, \(A_1=100A_2.\) That is, the first earthquake is 100 times more intense than the second earthquake.

How can we use logarithmic functions to compare the relative severity of the magnitude 9 earthquake in Japan in 2011 with the magnitude 7.3 earthquake in Haiti in 2010?

Solution.

To compare the Japan and Haiti earthquakes, we can use an equation presented earlier:

\(9−7.3=\log_{10}\left(\frac{A_1}{A_2}\right).\)

Therefore, \(A_1/A_2=10^1.7,\) and we conclude that the earthquake in Japan was approximately \(50\) times more intense than the earthquake in Haiti.

Checkpoint 1.135.

Compare the relative severity of a magnitude \(8.4\) earthquake with a magnitude \(7.4\) earthquake.

Hint.

\(R_1−R_2=\log_{10}\left(A_1/A_2\right).\)

Solution.

The magnitude \(8.4\) earthquake is roughly \(10\) times as severe as the magnitude \(7.4\) earthquake.

Subsection 1.8.2 Key Concepts

  • The logarithmic function \(y=\log_b (x)\) is the inverse of \(y=b^x.\) Its domain is \((0,\infty)\) and its range is \((-\infty,\infty).\)

  • The natural logarithmic function is \(y=\ln x=\log_e x.\)

  • Given an exponential function or logarithmic function in base \(a,\) we can make a change of base to convert this function to any base \(b\gt 0,b\neq 1.\) We typically convert to base \(e.\)

This book is a custom edition based on OpenStax Calculus Volume 1. You can download the original for free at https://openstax.org/details/books/calculus-volume-1. 2 

Additional practice exercises are available in at the bottom on this section in OpenStax Calculus Volume 1: https://openstax.org/books/calculus-volume-1/pages/1-5-exponential-and-logarithmic-functions

openstax.org/l/20_logscale
https://openstax.org/details/books/calculus-volume-1