(In 3, 4, 6, and 22 please follow the instructions exactly or you might not get credit. 3, 4 and 22 are intended to have you learn (by developing them) alternative ways to see concepts treated in the text by integration by parts and in my classroom notes by the surface interpretation. If all you do integrate by parts (in any of them) or use the surface interpretation (in 4) then you have not really developed an alternative way to solve the problem. The whole point of 6 is the interpretation in terms of stationary population; if you do not get to that you have missed the point of the project.)

NOTE: when a project is labeled speculative it means it could be very difficult: I might not even know the answer. If you work on a speculative project and don’t get an answer or a conclusion you can still get credit for the project. Show me the work you did and explain why you took the approaches you did, what seems to be going wrong and (if you know) why it seems to be going wrong, and what other ideas you might try (if any). If you have clearly done some thoughtful work on the project, that is enough to get credit.

#1 Critique the proof (a deliberately incorrect one) given in class that vanishing of y^kS(y) as y goes to infinity implies existence of the k-th moment (assume non-negative support).

#2 The surface interpretation shows that the size of a stationary population is proportional to the average lifetime (expectation of life at birth). Using areas and weights, what does the surface interpretation say about the size of a stably growing population (the rate of births at time t is B_t = B₀e^{k t} for some constant k)?

#3 Use the surface interpretation (i.e. do NOT integrate by parts anywhere in your work or you will get NO credit) and a little bit of algebra to write formulas for E[X^j(X_^d)^k] (or combinations thereof) for as many combinations of j=1,2,3,4 and k=1,2,3,4 as you can without using any powers higher than 4 in your answer. Assume non-negative support.

#4 Develop a purely algebraic method to express E[(X-d)₊^k] in terms of E[X^j] and E[(X_^d)^j] for j < k. Show how it works for k = 1, 2, 3, 4. Do NOT use the surface interpretation (as I do in class) and do NOT use integration by parts (as the textbook does) in any way or you will get NO Credit, but use only algebra and the definitions of the expressions involved. Forget that you know anything about surface interpretation or integration by parts. In fact, DO NOT use an integral anywhere in your work. Do NOT use the results from project #3; they depended upon surface interpretation. Assume non-negative support.

#5 Make three dimensional visual illustrations for the surface interpretation, including 2^nd and 3^rd moments and the relation of e(d), e²(d), and e³(d) to E[X],

E[X²], E[X³], E[X_^d], E[(X_^d)²], and E[(X_^d)³]. Assume non-negative support.

#6 For a continuous random variable X with non-negative support define a function L_X(u) by L_X(u)=E[X_Λu]. Find an expression for ∫_0,y L_X(u)du in terms of E[X_Λy] and E[(X_Λy)²]. Prove that ∫_0,∞S_X(u)e_X(u)du=E[X²]/2. Explain in words what that integral is telling us in a stationary population. Explain what E[X²]/(2E[X]) expresses in a stationary population, i.e. explain it purely in terms of population characteristics.

#7 Prove the Faa Formula without any advanced mathematics beyond the Taylor theorem. In particular, do not mention the Bell polynomials unless you define them, tell me about them, and prove whatever properties of Bell polynomials you want to use. (You do not have to use Bell polynomials at all, just think about the Faa problem and about the Taylor theorem.)

#8 Derive the Euler-Lagrange Differential Equation (rigorously). Explain any theorems or results that you use in the derivation (e.g. do not just say by the fundamental theorem of the calculus of variations without telling me exactly what the fundamental theorem of the calculus of variations is and what it means; by the way, you ought to be able to do it without even mentioning the fundamental theorem of the calculus of variations.). (see also #45)

#9 Working intuitively (rigorously would be hard to impossible) try to develop something like the no special treatment for any one value or set of values concept using arithmetic rather than geometric averages of the density values (hint: I wrote it down in class). Show how this might break down (fail to work or result in infinite answers) at some point in both the discrete and the continuous case. Conclude that the geometric average of the density values, leading to the maximum entropy principle, is one correct way to implement the concept of no special treatment for any one value or set of values. Come up with at least one other correct way to implement the concept and (speculative) see if you can explore what kind of distributions you get for some simple constraints.

#10 Derive the Laplace distribution using a system of two Euler Lagrange Differential Equations in two unknown functions f₁ and f₂, each one supported on only one side of the mean. (This is a slightly different question and problem to what we did in class! If you find yourself repeating your class notes you are on wrong track!)

#11 Attach your name to our no name random variable by finding the probability density function for the distribution with maximum entropy on -∞ to ∞ subject to the constraints (I) it is a probability density (II) the integral of (x-μ)f(x)dx over -∞ to ∞ is 0 (III) it has tail constraint function d(x)=ln{ln[e^{^}((x-μ)/b)+e^{^}(-(x-μ)/b]}, i.e. the integral of d(x)f(x)dx over -∞ to ∞ is one.

#12 Work out the definitions and properties (i.e. Appendix A) of a family of severity distributions analogous to the transformed beta family, but based upon transformations of the log-Laplace distribution rather than the log-logistic. You can let μ=0 in the log-Laplace for simplicity.

#13 Work out the definitions and properties (i.e. Appendix A) of a family of severity distributions analogous to the transformed beta family, but based upon transformations of the lognormal distribution rather than the log-logistic. You can let μ=0 in the lognormal for simplicity.

#14 Work out the definitions and properties (i.e. Appendix A) of a family of severity distributions analogous to the transformed beta family, but based upon transformations of the no-name distribution (from #11) rather than the log-logistic. You can let μ=0 in the no name for simplicity.

#15 (speculative) Work out (by working backwards) what constraints in a maximum entropy derivation correspond to each member of the transformed gamma and transformed beta families.

#16 (speculative) Work out (by working backwards) what constraints in a maximum entropy derivation correspond to the exponential-exponential distribution (the one with density e^xe^-exp(x))

#17 Work out what happens in the transformed beta and transformed gamma families if you replace the α-th conditional tail moment distributions:

Description: Description: Description: image002

with the α-th equilibrium distributions):

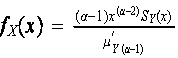
Description: Description: Description: image003

How do the resulting distributions differ from the gamma, transformed gamma, generalized Pareto, and transformed beta (that arose from the α-th conditional tail moment distributions)? How do the moments in App. A compare? Be very specific.

#18 Make a three dimensional visual illustration for the relationship below, and write down an interpretation in words.

#19 Work out the definitions and properties of a family of severity distributions analogous to the transformed beta family, but based upon transformations of the true inverse Gaussian distribution presented in class rather than the log-logistic.

#20 Work out the definitions and properties of a true inverse logistic, inverse logistic and reciprocal inverse logistic family of distributions, analogous to the true inverse Gaussian, inverse Gaussian and reciprocal inverse Gaussian presented in class.

#21 Work out the definitions and properties of a family of severity distributions analogous to the transformed beta family, but based upon transformations of any one (you pick one) of the inverse logistic family of distributions developed in project #20, rather than the log-logistic.

#22 Using surface interpretation (i.e. do NOT integrate by parts anywhere in your work or you will get No credit) and a little algebra work out formulas for E[X(X_^d)], E[X(X_^d)(X-d)₊], and 4E[X(X_^d)(X-d)₊²]-6E[X²(X_^d)²]. Assume non-negative support. Hint: compare with project #3.

#23 Prove (or, if a formal proof eludes you, just illustrate and discuss the connections) that the negative binomial is like a Poisson with contagion; i.e. the negative binomial with parameters (r,βt) gives the number of events in time t if the probability of one event in infinitesimal time t to t+dt, conditional on exactly m events having occurred from time 0 to time t, is equal to dt(rβ)((1+m/r)/(1+βt)). Try to make a similar interpretation of the binomial distribution.

#24 Work out the parameter space for the the (a,b,2) family of frequency distributions; include an analysis of the distributions on the line r = -1, analogous to the geometric (r = 1 in (a,b,0)) and logarithmic (r = 0 in (a,b,1)) distributions. Does any kind of interesting series summation arise (analogous to the geometric and logarithmic series)? Also work out the probability generating function on the line r= -1.

#25 Show (using probability generating functions) that a mixed Poisson distribution with infinitely divisible mixing distribution is also a compound Poisson, and give two specific examples of the phenomenon. Explain clearly why the infinite divisibility assumption is needed.

#26 (speculative) We have seen that the Negative Binomial can be the result of a Poisson mixture or of a compound Poisson. Can the Binomial distribution be the result of a Poisson mixture or of a compound Poisson? If so give an example and work out the parameters. If not, explain what goes wrong.

#27 Prove the Panjer recursion formula for an (a,b,1) primary distribution using the Faa formula.

#28 Come up with a spreadsheet (or other programming) algorithm to generate sets {j_k} with ∑_{(k=1, ∞)} j _k k = n, n=0,1, 2, etc. Is this efficient enough to warrant replacing Panjer recursion with direct use of the Faa formula to calculate compound distribution probabilities for (a, b, 0) primary distributions? Note that this would give you a calculation technique anytime the probability generating function of the primary distribution is known, whether or not there is a recursive feature to it. Is this an improvement versus brute force convolution?

#29 State and prove a usable generalization of the Faa Formula for the case of three nested functions.

#30 Develop recursive approximation formulae for E[(x-d)₊^3] in terms of E[(x-(d-h))₊^3], S, and lower moments of (x-d)₊; one formula for the discrete case (stair-step F) and one formula for the continuous case.

#31 Try to copy the development of ruin theory for the compound Poisson process using instead a compound Negative Binomial. Point out exactly what goes wrong. (speculative) Can you suggest or follow a way to keep going?

#32 (speculative) The equilibrium distribution, random variable X_e with density S_X(x)/μ_X is the solution to the following problem: (a) X is a given non-negative random variable (b) Y is an unknown non-negative random variable independent of X (c) Z is a random variable that follows the same probability distribution as Y (d) Y+Z= X|_X>Y. The solution to the problem is that Y and Z both follow the probability distribution of X_e. Note that X|_X>Y is a different random variable from X and that, as a result, it is not necessarily the case that Y is independent of X|_X>Y. Now here is the project: the k-th equilibrium distribution has Random Variable X_e₍_k) with density kx^k-1S_X(x)/ μ_X^k. Can you find a similar problem to which X_e₍_k) is the solution?

#33 (speculative and difficult) Can you prove that the maximum entropy probability density with the same constraints as gave rise to the Laplace density, but also with the additional constraint that the density should be smooth (continuous derivatives of all order) at x=μ, must be the logistic density? If it is not the logistic, then what is it?

#34 Work out the definitions and properties of a true inverse exponential-exponential, inverse exponential-exponential and reciprocal inverse exponential-exponential family of distributions, analogous to the true inverse Gaussian, inverse Gaussian and reciprocal inverse Gaussian presented in class, but based upon the exponential-exponential distribution (with density e^xe^-exp(x) ) rather than the standard normal. Be careful! Unlike the standard normal, the exponential-exponential is not symmetric.

#35 Work out the definitions and properties of a family of severity distributions analogous to the transformed beta family, but based upon transformations of any one (you pick one) of the inverse exponential-exponential family of distributions developed in project #34, rather than the log-logistic.

#36 In the (a,b,0) family of frequency distributions perform an analysis of the distributions on the lines r = 2 and r=3, analogous to the geometric (r = 1 in (a,b,0)) and logarithmic (r = 0 in (a,b,1)) distributions. Are there any special properties of the r=2 and r=3 distributions. Do any kind of interesting series summations arise (analogous to the geometric and logarithmic series)? Also work out the probability generating functions on the line r= 2 and r=3.

#37. Work out what constraints in a maximum entropy problem will give rise to the true inverse Gaussian distribution.

#38 (speculative) Using the formula in project #18 (whether or not you have done project #18 does not matter, just take that formula) try to connect the behavior of CTE(q) as q varies to the concepts increasing mean excess loss = heavy tail and decreasing hazard ratio = heavy tail.

#39 In the description of the random variable Y=X_e following the equilibrium distribution in project #32, what distribution that we have studied does the random variable X|_X>Y follow?

#40 (speculative) In project #32, for the random variable X_e_(k) that follows the k-th equilibrium distribution, is there a random variable W where X|_X>W plays a similar role to that played by X|_X>Y for the equilibrium distribution? What distribution does the random variable X|_X>W follow? Have we studied it?

#41 Look at a tail-weight measure defined by lim_x_→∞(∫_x^∞S_X(y)dy)/ (∫_x^∞S_Y(y)dy). Work out its relationships to all the other tail measures, such as limiting tail weight ratio, mean excess loss function, hazard rate function, moments, and anything else you can think of.

#42 (speculative) By working backwards, figure out what constraints on a maximum entropy problem will give rise to the general form of a linear exponential distribution with non-negative support. Note whether there are any special problems or conditions involved. The linear exponential distribution with non-negative support has density function f(x)=(a+bx)exp(-ax-(b/2)x²).

#43 (speculative) Work out as closely as you can an exact description of which random variables X give rise to exponential transformations Y=e^X that are NOT heavy-tailed.

#44 (speculative) Work out exactly the conditions on a heavy-tailed random variable X that would allow the α-shaping Y of X defined by S_Y(y)=S_X(y)^α to have a lighter mean-adjusted tail than X for α<1 and a heavier mean-adjusted tail than X for α>1.

#45 Explain in words and/or pictures why the Euler-Lagrange Differential Equation is intuitively believable. Do not just give a proof! (that is project #8) For this project, I want pictures and/or explanations of why it seems sensible.

#46 Prove that lim_x→∞e(d)=1/( lim_x→∞h(d)) and illustrate it with a picture or diagram.

#47 (speculative) Find a simpler proof that for the (a,b,0) family with a>=1 and b<0 it must be that a+b=1. Simpler means a proof that does not involve lim_k→∞Σ_j_=k,∞p_j>=1

Typical Assignments (most recent at top)(from 3^rd edition of Loss Models)

Study the Two Ruin Theory Notes above and the spreadsheet example for ruin probabilities

Sec. 11.1-11.4 and exerc. 11.1-11.3, 11.6-11.7, 11.9-11.18

Sec. 10.1-10.2

Study the Stop-Loss Example and Spreadsheet above … be able to do such problems independently

Study the EXCEL examples and distribution fitting examples above and be able to do such calculations independently.

Sec. 9.8-9.12 and exerc, 9.47-9.65, 9.67-9.69

Sec. 9.1-9.7 and exerc. 9.1-9.36

Sec. 6.10-6.13 and 8.6. Exer.6.20-6.28, 6.32, 8.29-8.34

Sec. 6.7-6.9 and exerc. 6.10-6.19

Sec. 6.1-6.6 and exer. 6.1-6.9 and use Faa’s formula to calculate the first 4 raw and central moments of the Poisson, Neg. Binomial, and Binomial distributions

Validate (comparing formulas is good enough, but surface interpretation is interesting so you might want to try it) that if X is a log-logistic then the k-th conditional tail moment distribution of X is a transformed beta (or, when γ=1, a generalized Pareto)

Sec. 3.4 and 3.5; exer.3.25 to 3.37 (Beware some misprints in both the text and the solution manual. See errata!)

Write down a formula for the 3^rd moment analogous to Theorem 8.8

Be sure that you can see Theorems 8.3, 8.5, 8.6, 8.7 and 8.8 in terms of the surface interpretation

Sec. 8.1-8.5 and exer. 8.1-8.28 (In chapter 8 try to think in terms of the surface interpretation. It will simplify everything)

Study the Maximum Entropy paper (download above)

Sec. 5.4-5.5 and exer. 5.24-5.27

Sec. 5.1-5.3 and exer. 5.1-5.23 (keep a bookmark in appendix A!)

Sec. 4.1-4.2 and exer. 4.1-4.12

Sec. 3.3 and exer. 3.21-3.24

Sec. 3.1-3.2 and Exer. 3.1-3.20

Ch. 1&2 and Exer.2.1-2.5