Math 395 Risk Theory
Instructor – James G. Bridgeman
Maximum Entropy Paper (K. Conrad) EXCEL Example for Convolution (see page 145)
(note use of the EXCEL functions OFFSET and SUMPRODUCT)
EXCEL Example for Panjer Recursion (try convolution on this one first!)
Stop-Loss Example Stop Loss Example Spreadsheet
Distribution fitting example (pp144-45)
Example of Compound Geometric and Panjer Recursion For Ruin Probabilities
FINAL EXAM (due back 12-14 5PM) ****note a typo in #2 was corrected at 3 pm on
12-12: reference is to problem #1, not 5*****
Final Exam Solutions Final
Exam Solution Spreadsheet Grading Worksheet
Not required at all, but if you wanted additional background and context you can read Sec. 6.8-6.10 and Sec. 8.5.
Cumulative Assignments (Final)
Sec. 8.1-8.4 and exerc. 8.1-8.3, 8.6-8.7, 8.9-8.18
Sec. 7.1-7.2
Study the Stop-Loss Example and Spreadsheet above … be able to do such problems independently
Exerc. 6.29-6.35, 6.37-6.58
Sec. 6.5-6.7
For the example on pages 143 to 145 (same as convolution
example above) find each of the 5 two parameter distributions (normal,
lognormal, inverse Gaussian, gamma, Pareto) that best fits the mean and
variance of the aggregate losses. Which
of the 5 is the best choice? Hand in this work on the
28th
Sec. 6.1-6.4 and exer. 6.1-6.27
Sec. 4.6.10-4.6.11, 5.6 and exer. 4.56-4.60, 4.62,5.24-5.27
Sec. 4.6.7-4.6.9 and Exer. 4.41-4.47, 4.50-4.55
Calculate the coefficients of variation, skewness and kurtosis for the Poisson, Neg. Binomial, and Binomial distributions
Sec. 4.6.1-4.6.6 and exer. 4.40, 4.42-4.49, and use Faa’s formula to calculate the first 4 raw and central moments of the Poisson, Neg. Binomial, and Binomial distributions
Validate (comparing formulas is good enough, but surface interpretation is interesting so you might want to try it) that if X is a log-logistic then the k-th conditional tail moment distribution of X is a transformed beta (or, when γ=1, a generalized Pareto)
Determine the coefficient of skewness in example 5.15 (surface interpretation!)
Write down the formula for the 3rd moment analogous to Theorem 5.14 (surface interpretation!)
Sec. 5.1 – 5.5 and exer. 5.1 to 5.23 (in ch. 5 try to think in terms of the surface interpretation)
Sec. 4.5 and exer. 4.37-4.39
Exer. 4.33-4.36
Sec. 4.3-4.4 and exer. 4.13-4.32 (keep a bookmark in appendix A!)
Sec. 4.1-4.2 and exer. 4.1-4.5, 4.7-4.9, 4.11-4.12
Sec. 3.3 and exer. 3.20-3.24
Sec. 3.1-3.2 and Exer. 3.1-3.19
Project Topics: (pick any four to submit by end of semester … topics will be added as we go)
#1 Critique the “proof” given in class that vanishing of y kS(y) as y goes to infinity implies existence of the k-th moment (assume non-negative support and nice behavior for y near 0)
#2 The surface interpretation shows that the size of a stationary population is proportional to the average lifetime (expectation of life at birth). What does the surface interpretation say about the size of a stably growing population (the rate of births at time t is Bt = B0ek t for some constant k)?
#3 Develop a purely algebraic method to express E[(X-d)+k] in terms of E[Xj] and E[(X^d)j] for j < k. Show how it works for k = 1, 2, 3, 4. Do not use the surface interpretation (as I do in class) and do not use integration by parts (as the textbook does)
#4 Make three dimensional visual illustrations for the surface interpretation, including 2nd and 3rd moments and the relation of e(d), e2(d), and e3(d) to E[X],
E[X2], E[X3], E[X^d], E[(X^d)2], and E[(X^d)3].
#5 See handout on LX(u)=E[x^u]. Answer the series of questions. (Think of a stationary population).
#6 Make a three dimensional visual illustration for the relationship below, and write down an interpretation in words.
![]()
#7 Prove Faa’s Formula.
#8 Work out the definitions and properties of a family of severity distributions analogous to the transformed beta family, but based upon transformations of the log-Laplace distribution rather than the log-logistic.
#9 Work out the definitions and properties of a family of severity distributions analogous to the transformed beta family, but based upon transformations of the lognormal distribution rather than the log-logistic.
#10 (speculative) Work out what constraints in a maximum entropy derivation correspond to each member of the transformed gamma and transformed beta families.
#11 Work out what happens in the transformed beta and transformed gamma families if you replace the α-th conditional tail moment distributions:
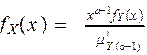
with the α-th equilibrium distributions):
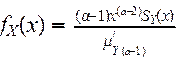
How do the resulting distributions differ from the gamma, transformed gamma, generalized Pareto, and transformed beta (that arose from the α-th conditional tail moment distributions)?
#12 Work out the definitions and properties of an inverse logistic and reciprocal inverse logistic family of distributions, analogous to the inverse Gaussian and reciprocal inverse Gaussian presented in class.
#13 Work out the definitions and properties of a family of severity distributions analogous to the transformed beta family, but based upon transformations of the inverse logistic distribution developed in project #12.
#14 Work out the definitions and properties of a family of severity distributions analogous to the transformed beta family, but based upon transformations of the true inverse Gaussian distribution presented in class rather than the log-logistic.
#15 Prove (or, if a formal proof eludes you, just illustrate and discuss the fact) that the negative binomial is like a Poisson with contagion; i.e. the negative binomial with parameters (r,β) gives the number of events in unit time if the probability of one event in infinitesimal time dt, conditional on exactly m events having occurred from time 0 to time t, is equal to dt(rβ)((1+m/r)/(1+βt)). Try to make a similar interpretation of the binomial distribution.
#16 Show (using probability generating functions) that a mixed Poisson distribution with infinitely divisible mixing distribution is also a compound Poisson, and give two specific examples of the phenomenon.
#17 Prove the Panjer recursion formula for an (a,b,1) primary distribution using Faa’s formula.
#18 Come up with a spreadsheet (or other programming) algorithm to generate sets {j k} with ∑ (k=1, ∞) j k k = n, n=0,1, 2, … Is this efficient enough to warrant replacing Panjer recursion with direct use of Faa’s formula to calculate compound distribution probabilities for (a, b, 0) primary distributions? Note that this would give you a calculation technique anytime the probability generating function of the primary distribution is known, whether or not there is a recursive feature to it. Is this an improvement versus brute force convolution?