Triple Integrals and Spherical Coordinates
Copyright © 1999, 2001 by James F. Hurley, University of Connecticut Department of Mathematics, Unit 3009, Storrs CT 06269-3009. All rights reserved.
1. Using the basic
sphereplot
command
. Rcall that Maple's
command
sphereplot
produces immediate plots of surfaces with equations of the form
![]() =
f
(
=
f
(
![]() ,
,
![]() )
. The syntax is
)
. The syntax is
sphereplot( f(
![]() ,
,
![]() ),
),
![]() =
=
![]() ..
..
![]() ,
,
![]() =
=
![]() ..
..
![]() )
;
)
;
This basic
command is designed to plot spherical-coordinate equations that are solvable for the radial variable Ñ in this case,
![]() Ñ and are swept out as the angles
Ñ and are swept out as the angles
![]() and
and
![]() vary over a basic spherical-coordinate region ("spherical-coordinate rectangle") [
vary over a basic spherical-coordinate region ("spherical-coordinate rectangle") [
![]() ,
,
![]() ]
´
[
]
´
[
![]() ,
,
![]() ] in the
] in the
![]()
![]() -plane. It thus can plot only one of the three basic equations
coordinate variable
=
constant
, namely the sphere
-plane. It thus can plot only one of the three basic equations
coordinate variable
=
constant
, namely the sphere
![]() =
k.
=
k.
Just as for the basic
cylinderplot
command, the basic version of
sphereplot
is powerful enough to give useful plots of many simple regions that arise in spherical-coordinate integration. The following example considers a triple integral that, in Cartesian coordinates, would be quite formidable.
Example 1
. Evaluate
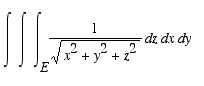 , where E is the region between the two spheres
, where E is the region between the two spheres
![]() and
and
![]() .
.
Solution.
The region is easy to visualize, and to plot if we restrict the angle
![]() t
o the range [0, ¹], so that removal of the (hidden) sphere of smaller radius does not eliminate it from view. The following routine is just a slight modification of the last one.
t
o the range [0, ¹], so that removal of the (hidden) sphere of smaller radius does not eliminate it from view. The following routine is just a slight modification of the last one.
>
with (plots):
surf1 := sphereplot (2, theta = 0..Pi, phi = 0..Pi, axes = boxed, scaling = constrained):
surf2 := sphereplot (3, theta = 0..Pi, phi = 0..Pi, axes = boxed, scaling = constrained):
xaxis := spacecurve([t, 0, 0, t = -2..3.5, color = magenta]) :
yaxis := spacecurve([0, t, 0, t = -2..3.5, color = magenta]) :
zaxis := spacecurve([0, 0, t, t = -2..3.5, color = magenta]) :
labx := textplot3d([3.6, 0, -.2, `x`], color = magenta):
laby := textplot3d([0,3.6, -.2, `y`], color = magenta):
labz := textplot3d([0, 0, 3.6, `z`], color = magenta):
display(surf1, surf2, xaxis, yaxis, zaxis, labx, laby,labz);
![[Maple Plot]](images/SphericalTripInts26.gif)
An arrow (like the
x
-axis) shot radially outward from the origin enters the region
E
by passing through the sphere of radius 2, and then exits
E
through the sphere of radius 3. Thus,
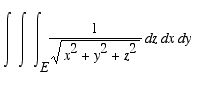 =
=
![Int(Int(Int([1/rho]*rho^2*sin*phi,rho = E .. ``),ph...](images/SphericalTripInts28.gif)
=
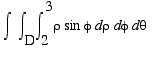
=
![Int(Int([1/2]*[9-4]*sin*phi,phi = D .. ``),theta = ...](images/SphericalTripInts30.gif) ,
,
where the region
D
is the "spherical-coordinate
![]()
![]() -rectangle" [0, 2¹]
´
[0, ¹]. Hence, the value of the triple integral is
-rectangle" [0, 2¹]
´
[0, ¹]. Hence, the value of the triple integral is
![Int(Int([5/4]*sin*phi,phi = D .. ``),theta = `` .. ...](images/SphericalTripInts33.gif) =
=
![Int(Int([5/2]*sin*phi,phi = 0 .. Pi),theta = 0 .. 2...](images/SphericalTripInts34.gif) =
=
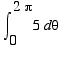 = 10¹.
= 10¹.
As before, Maple can check the evaluation, via the
TripleInt
command in its
student
package.
>
with (student):
value(Tripleint(rho*sin(phi), rho = 2..3, phi = 0..Pi, theta = 0..2*Pi) );
![]()
2. More general regions
.
Recall that the
sphereplot
command Ñ in a slightly modified form Ñ can plot the graphs of surfaces whose equations are not of the basic form
![]() =
f
(
=
f
(
![]() ,
,
![]() )
. The syntax of the extended
sphereplot
command requires specification of the formulas for all three variables
)
. The syntax of the extended
sphereplot
command requires specification of the formulas for all three variables
![]() ,
,
![]() and
and
![]() .
The syntax for the extended
sphereplot
command is
.
The syntax for the extended
sphereplot
command is
sphereplot( [
![]() ,
,
![]() ,
,
![]() ], u =
], u =
![]() ..
..
![]() , v =
, v =
![]() ..
..
![]() )
;
)
;
As with the extended
cylinderplot
command, in this expression the generic symbols
u
and
v
stand for the two independent parameters among
![]() ,
,
![]() , and
, and
![]() that vary to define the surface in question. The next example illustrates the usefulness of the extended
sphereplot
command by revisiting the first example of the Cylindrical Triple Integral handout.
that vary to define the surface in question. The next example illustrates the usefulness of the extended
sphereplot
command by revisiting the first example of the Cylindrical Triple Integral handout.
Example 2
. Find the volume of the region
E
above the graph of
z
=
![]() and below the graph of
and below the graph of
![]() = 4.
= 4.
Solution
. The first step is to plot the region
E
between the cone and the sphere, which of course has the simple spherical-coordinate equation
![]() = 2. What is the equation of the cone in spherical coordinates? Recall that
= 2. What is the equation of the cone in spherical coordinates? Recall that
z
=
![]() cos
cos
![]()
and
![]() =
r
(of cylindrical Ñ or polar Ñ coordinates). In deriving the formulas for changing coordinates from spherical to rectangular coordinates, a key relation is
=
r
(of cylindrical Ñ or polar Ñ coordinates). In deriving the formulas for changing coordinates from spherical to rectangular coordinates, a key relation is
r
=
![]() sin
sin
![]() .
.
The equation
z
=
r
of the cone thus transforms to
![]() cos
cos
![]() =
=
![]() sin
sin
![]() Þ
1 = tan
Þ
1 = tan
![]() Þ
Þ
![]() =
=
![]() .
.
The following routine generates a plot of the region
E
without the need Ñ which arose in plotting
E
via cylindrical coordiantes Ñ to determine algebraically the curve of intersection of the sphere
![]() = 2 and the cone
= 2 and the cone
![]() =
=
![]() .
Execute the routine, and then experiment by rotating it to produce a good view.
.
Execute the routine, and then experiment by rotating it to produce a good view.
>
with (plots):
surf1 := sphereplot (2, theta = 0..Pi, phi = 0..Pi/2, axes = boxed):
surf2 := sphereplot ([rho, theta, Pi/4], rho = 0..2, theta = 0..Pi):
xaxis := spacecurve([t, 0, 0, t = -2..2.5, color = magenta]) :
yaxis := spacecurve([0, t, 0, t = -2..2.5, color = magenta]) :
zaxis := spacecurve([0, 0, t, t = -1..2.5, color = magenta]) :
labx := textplot3d([2.6, 0, -.2, `x`], color = magenta):
laby := textplot3d([0,2.6, -.2, `y`], color = magenta):
labz := textplot3d([0, 0, 2.6, `z`], color = magenta):
display(surf1, surf2, xaxis, yaxis, zaxis, labx, laby,labz, scaling = constrained);
![[Maple Plot]](images/SphericalTripInts71.gif)
An arrow shot radially outward from the origin through
E
emerges from the sphere
![]() = 2
.
Bearing in mind that
dV
=
= 2
.
Bearing in mind that
dV
=
![]() d
d
![]() d
d
![]() d
d
![]() ,
the volume is then
,
the volume is then
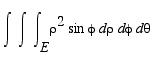 =
=
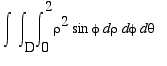 =
=
![Int(Int([8/3]*sin*phi,phi = D .. ``),theta = `` .. ...](images/SphericalTripInts79.gif)
=
![Int(Int([8/3]*sin*phi,r = 0 .. Pi/4),theta = 0 .. 2...](images/SphericalTripInts80.gif) =
=
![]() .
.
Maple's
TripleInt
command from the
student
package agrees with this calculation:
>
with (student):
value(Tripleint(rho^2*sin(phi), rho = 0..2, phi = 0..Pi/4, theta = 0..2*Pi) );
![]()