Double Integrals and Polar Coordinates

Copyright © 2001by James F. Hurley, University of Connecticut Department of Mathematics, Unit 3009, Storrs CT 06269-3009. All rights reserved.

1. Plots via polarplot . Maple's plots library includes the command polarplot , which directly plots curves with polar-coordinate equations r = f ( ) . (It can also plot polar-coordinate equations parametrically: refer to Maple's Learning Guide or on-line Help .) The syntax of the polarplot command is

polarplot( f( ), = .. ) ;

The following routine illustrates it for the circle r = 4. Note inclusion of the command scaling = constrained to make the circle appear circular (rather than elliptical). Also note that the default plot shows the x - and y -axes. That is handy, because in most cases polar coordinates arise in double integrals when a given xy -region is simpler to describe and integrate over in polar coordinates. Execute the routine by placing your cursor at the end and hitting the Enter key.

> with (plots):
polarplot (4, theta = 0..2*Pi, scaling = constrained);

2. Polar Coordinates and Double Integrals . Exercise 12 from Section 16.4 of James Stewart, Calculus, 4th Edition , ITP Brooks/Cole, 1999, illustrates the simplification that change to polar coordinates can bring to evaluation of double integrals.

Example 1 . Evaluate the double integral of f ( x , y ) over the disk ² 16 if


.

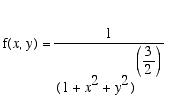
Solution . The formula for the integrand is quite involved, but changing to polar coordinates transforms it to a much simpler form in which the denominator becomes ( ) to the power 3/2. Hand evaluation of the resulting integral

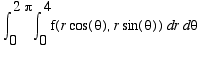
gives , which you can ask Maple to check with its Doubleint command in the student package.

> with (student):
value( Doubleint( 1/(1 + r^2)^(3/2), r = 0..4, theta = 0..2*Pi) );

Oops! What went wrong? The hand calculation? No, actually the Doubleint command has a serious limitation: it works only for Cartesian-coordinate integrals ! So you must manually supply the factor r in the formula

dA = r dr d

and have Maple evaluate the iterated integral as in the routine below.

> with (student):
value(Doubleint(r/(1 + r^2)^(3/2), r = 0..4, theta = 0..2*Pi) );

As you should confirm, that agrees with the hand calculation.